Constraint Programming 101
Constraint Programming (CP) is a declarative paradigm of programming, which represents problem by specifying features required from its solutions. The programmer has to:
define all variables occurring in the problem along with theirs domains;
define constraints on the introduced variables, which have to be satisfied by the solutions;
[optional] define optimality criteria, e.g. cost function, which has to be minimized;
[optional] define the search procedure which will be used to find the solution.
All files required to solve the assignments are available via the repository, so clone it first and follow the Readme instructions.
"Real Life" Example
Let's pretend, that we work as a waiter in a restaurant very close to the university campus. One sunny lazy day, there was a computer science conference going on at the campus, and during the lunch break our restaurant has been attacked by an horde of hungry nerds. One of them was particularly vicious and he gave us a very stupid order:
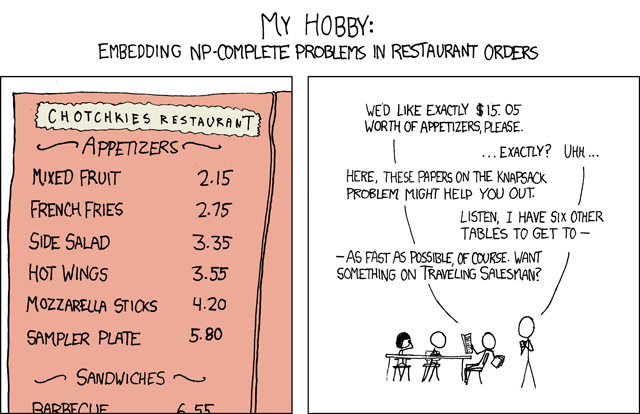
The situation appeared hopeless as the problem is non polynomial… Luckily we've heard of constraint programming and without any hesitation started to solve the problem!
Software
Install MiniZinc bundle according the the
instructions. It should be already installed on the C2/316 computers.
Run MiniZinc IDE
Solving the Problem
Modelling problem in MiniZinc consists of four steps:
1. First Step: Variables
Our goal is to complete the insane order. Every order consists of meals, where every meal may be ordered more than once. Let's assume that man can't order half of the meal. Let's define one variable per meal and define their domains as integers. Every variable indicates how many times the meal occurs in the order. In MiniZinc one would write (note the var keyword):
var int: fruit;
var int: fries;
var int: salad;
var int: wings;
var int: sticks;
var int: sampler;
2. Second Step: Constrains
We can be fairly sure that man can't order a negative amount of meals. We can code it in MiniZinc using constraint keyword:
constraint fruit >= 0;
constraint fries >= 0;
constraint salad >= 0;
constraint wings >= 0;
constraint sticks >= 0;
constraint sampler >= 0;
Moreover we know, that the order has to have a specific price. In order to avoid floats we will multiply all the prices by 100.
constraint fruit*215 + fries*275 + salad*335 + wings*355 + sticks*420 + sampler*580 == 1505;
3. Step Three: Goal
We are looking for an order that satisfies the constrains. The solve keyword defines the goal.
solve satisfy;
4. Output
Finally we have to define, how to present results to the user. We use the output keyword:
output ["fruit:", show(fruit), "\t fries:", show(fries),
"\t salad:", show(salad), "\t wings:", show(wings),
"\t sticks:", show(sticks), "\t sampler:", show(sampler)];
Running Code
The simplest way: MiniZincIDE → Menu → Minizinc → Run.
To receive more than one solution, check the Show configuration editor button in the right top corner, check the User-defined behavior checkbox and select Print all solutions.
X
Tip 50%
The comic strip claims, that we will receive a tip only if we manage to create a general solution. We like tips, so let's get to work!
1. First Step: Parameters
Let's begin with defining the menu's structure, how many different meals are in there? Notice lack of the var keywords. It's not a variable, it's a constant parameter.
int: menu_length = 6;
Then, what is the required price of the order:
int: money_limit = 1505;
Next, we will use arrays to describe the menu's contents. Every array has defined a set of indexes and type of the elements:
array[1..menu_length] of int: menu_prices = [215, 275, 335, 355, 420, 580];
array[1..menu_length] of string: menu_names = ["fruit", "fries", "salad", "wings", "sticks", "sampler"];
2. Second Step: Variables
In the general version, there should be as many variables as there is meals in the menu:
array[1..menu_length] of var int: order;
3. Third step: Constraints
Number of the constraints also depends on the menu's size. To define constraints we will use aggregating functions: forall — concatenates all the constraints in a table, sum — sums numbers in a table. We will also use an array comprehension, which processes the elements of an array according to the defined operation and index set, e.g. [array[i]*2 | i in 1..array_length] return an array with all the values multiplied by 2. The pipe operator | separates operation and index set we iterate over.
constraint forall([order[i] >= 0 | i in 1..menu_length]);
constraint sum([order[i] * menu_prices[i] | i in 1..menu_length]) == money_limit;
4. Fourth Step: Goal
5. Fifth Step: Output
Again we will use array comprehension. The double-plus operator concatenates strings, while the show function converts number to a string.
output [menu_names[i] ++ ": " ++ show(order[i]) ++ "\n" | i in 1..menu_length];
Running Code
No changes here. Please run the code, and spent the imaginary tip wisely.
Mixing parameters and variables is not a good practice — every time the menu changes we would have to modify the program. To solve this issue we can define the parameters' values in the separate data files. Please create a data file (MiniZincIde → File → New data) with contents:
menu_length = 6;
money_limit = 1505;
menu_prices = [215, 275, 335, 355, 420,580];
menu_names = ["fruit", "fries", "salad", "wings", "sticks", "sampler"];
Then please remove the parameters' values from the program. Leave only the empty declarations, e.g. replace int: menu_length = 6; with int: menu_length;.
Running Code
When you hit the run, you should be prompted to fill the missing values. You could do it by hand, but I strongly recommend to choose a data file from the drop down list. The data file has to be opened in the IDE.
The Wallet Problem
So far we had only to satisfy the problem. There exist to different kinds of goals in the MiniZinc language: maximize <expression> and minimize expression, both are used to define the optimality criteria, e.g.
solve minimize sum(order);
modifies our problem to look for an order with the lowest amount of meals.
Assignments
Please add another parameter called yumyum_factors. It should be an array of integers, which say how much we like a particular meal (bigger the number is, more we like the meal).
We are looking for a solution, which maximizes the sum of the yumyum factors in our order.
We don't have to spend all the money we have.
Polishing rough edges
Now we should have a basic working model for the problem at hand, but there are still few ways to improve it.
Also this is a good moment to play with the MiniZinc compiler — how to debug and find faults in the model.
Assignments
Can you think of more succinct way to assert that you can't buy negative number of meals? Currently we use constraints >= 0 - remove them.
We should make sure that our model won't accept illegal parameters. Try special debugging functions to debug your program and assert your requirements. Try functions below, they can prove to be pretty useful in the future:
abort(“Message”)
trace(“Message”)
assert(<test>, “Message”)
trace(“Message”, <expression>)
assert(<test>, “Message”, <expression>)
where:
<test> is something like x < 3
<expression> may be a constraint or anything that returns a value
you can use double-plus and show to build more complicated messages
Ranges, e.g.
1..menu_length are special cases of
sets. Replace all the ranges with named sets to avoid code duplication. The declaration should like this:
set of <type>: SetName = start..end;
Show configuration editor is a very tempting button in the right top corner of the MiniZincIDE. Play with the options:
