Automated Planning: 101
Due to the COVID-19 outbreak, all files related to this class are stored in the Gitlab repository. This class uses files stored in the 00_intro folder. Please refer to the Readme.md on how to submit the solutions.
This class is an introduction to a very important and omnipresent (i.e.: industry, robotics, video games etc.) discipline of AI – planning. Planning consists in finding a series of actions (called “a plan”), which used on a initial state S will conclude in achieving goal state G. Every action has conditions in which it can be executed, and effects of its application. Planning is difficult: without adequate constraints on actions, the complexity reaches the PSPACE-complete class (worse than NP problems class, which includes the problems of discrete optimization). Furthermore, real (not toylike) problems may contain additional factors increasing their difficulty:
Incomplete knowledge about actual state. For example, the lack of appropriate sensors in a robot, or a card game, where we don’t know the whole hand, but we must plan our moves in advance (like in bridge)
Uncertainty resulting from unreliability of actions. In this case we are not sure if used action will succeed. A simple model is a RPG game, where a roll of dice decides the success of an action. A plan of a battle should take into account the possibility of unsuccessful roll.
Execution of an action takes time. The plan should take into account the temporal aspect of the problem. Our environment rarely stays static and friendly.
Possibility of events independent from the agent – i.e.: a car crush in front of an automated car. Handling of such exceptions also comes within the scope of planning.
In view of its basic character, this class will cover the difficult question of classical planning.
Blocks World
An old and popular problem of classical planning is so called “blocks world”. The problem doesn’t seem very ambitious: it consists in finding a correct sequence of moves enabling shifting blocks from initial stage to a given goal state. There is a specified number of blocks in “blocks world” (traditionally, a block can be distinguished by letter written on it), and several columns, where the blocks can be positioned. Every block either lies on the bottom of a column (“on the table”), or is put on the top of another block. An example of initial and goal state is given in the above picture. There are two possible actions in the blocks world:
Picking a block up by a robot. This action can be executed if the block is accessible (there are no others blocks on its top) and the robot’s arm is empty (only one block can be picked up at a time)
Putting a block down by a robot. This action can be executed if the robot’s arm is not empty. A block can only be put on the top of a column.
Solutions
There are three relatively simple solutions to this problem:
A-star
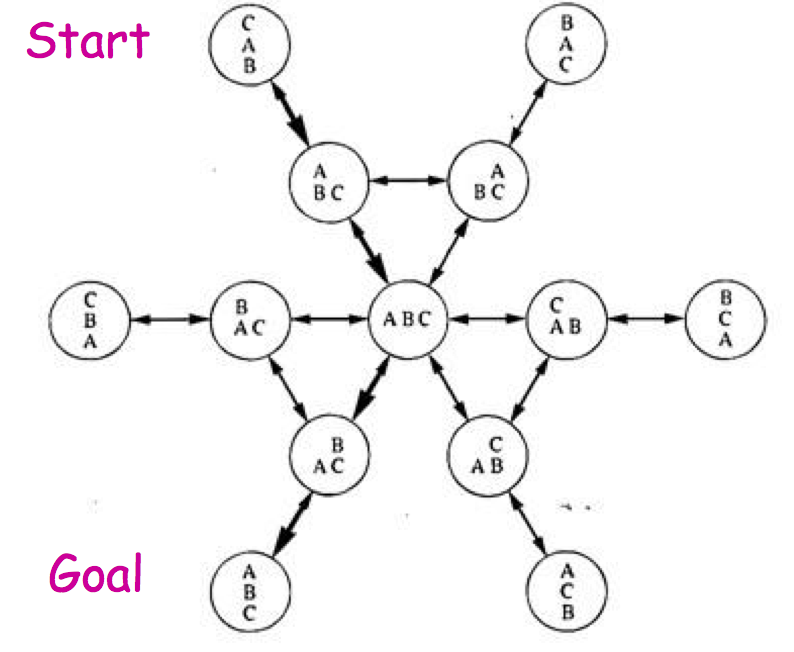 A standard representation of the planning problems is a directed graph called “state space” – every node in the graph correspond to a possible state of the world. Two nodes are connected by edge, if there exist an action, which enables moving from one state to another. The planning problem consists in this case in finding a path connecting given node (initial state) with the other (goal state). The state space is often enormous (potentially infinite), and there are no obvious methods of conducting a search. An example of a state space for a very simple instance of a blocks world problem is given below.
A standard representation of the planning problems is a directed graph called “state space” – every node in the graph correspond to a possible state of the world. Two nodes are connected by edge, if there exist an action, which enables moving from one state to another. The planning problem consists in this case in finding a path connecting given node (initial state) with the other (goal state). The state space is often enormous (potentially infinite), and there are no obvious methods of conducting a search. An example of a state space for a very simple instance of a blocks world problem is given below.
Assignments
Encoding as a Discrete Optimization Problem
Very often it is possible to translate a planning problem to a corresponding discrete optimization problem and then use discrete optimization techniques, e.g. constraint programming. This kind of translation is however limited:
we have to model the timeline; every moment requires a corresponding variables to store the state and action;
the timeline has to be finite; we don't know in advance what is the length of the plan but in discrete optimization we have to specify fixed amount of variables. Therefore we often create redundant variables, making timeline “long enough”.
Assignments
-
the blocks worlds defined in the model is simplified. Can you find the differences between model and the problem stated before?
which constraint defines state transitions?
please introduce following changes to the model:
increase maximal length of the plan — what influence it has on the solution?
change the domain of the last step (end) from int to something more constrained
change constraint defining the state transitions, so the transitions won't occur after the time stated in the end variable '
use search annotations, so the solver would start search with the smallest end possible and increase it later
fix the output to display only relevant states
Planner
Other (the simplest) approach is to use an existing planning software. In the 70' Stanford has introduced the famous STRIPS solver. It's a bit old but the knowledge representation used there is still relevant and is often called a STRIPS representation. The STRIPS problem is represented as:
The simple planner may work according to the crude algorithm (G is the goal state, and S is the initial state):
Initiate stack to store the plan.
Check if the current state is equal to G. If yes, display the plan and exit.
Find fact F, which is true in G and false in the current state.
Find action A, which has F on the list of the added facts.
Remove A from the list of available actions (why?).
Call recursively planning routine to find plan P that goes to state, that satisfies the conditions of A.
Reintroduce A to the list of available actions.
Push elements of P and A on stack
Execute the plan and then action A to update the current state.
Restart the planning routine from the new state.
The algorithm's result will be a reversed plan.
Assignments

Check
a simple STRIPS planner for the blocks worlds. If you know Prolog, read the last lines of the file to understand how the planner works. If you haven't seen Prolog before, don't panic, keep calm and go to the next assignments.
Fill %TODO: sections:
every state is represented by five types of facts (example states are available in the EXAMPLES OF USAGE):
ontable/1 — block lies on a table, e.g. ontable(a) means that block a lies on a table
on/2 — block lies on another block, e.g. on(a,b)
clear/1 — there is nothing lying on the block, e.g. clear(a)
holding/1 — block is currentle held by the robotic arm, e.g.. holding(a)
handempty/0 — the robotic arm doesn't hold anything, e.g. handempty
we need four actions (one of them is already implemented)
put block X on block Y:
requires that the X is actually held in the robotic arm and Y is clear. After performing the action X lies on the Y and Y is no clear anymore. Also the robotic arm doesn't hold anything.
take block X off the Y:
requires that X is clear and lies on the Y. After performing the action, block X is no clear anymore; it doesn't lie on the Y anymore and it is held in the arm. Also Y becomes clear.
put block X on the table:
simpler version of the first action
take X of the table:
simpler version of the seciond action
Run planning on the three already specified problems (just write problem1. or problem2.… in the query window on the right and hit run.
Specify fourth custom problem.
Remove clear conditions from every action and repeat the planning:
is there any value in such plans?
-
 A standard representation of the planning problems is a directed graph called “state space” – every node in the graph correspond to a possible state of the world. Two nodes are connected by edge, if there exist an action, which enables moving from one state to another. The planning problem consists in this case in finding a path connecting given node (initial state) with the other (goal state). The state space is often enormous (potentially infinite), and there are no obvious methods of conducting a search. An example of a state space for a very simple instance of a blocks world problem is given below.
A standard representation of the planning problems is a directed graph called “state space” – every node in the graph correspond to a possible state of the world. Two nodes are connected by edge, if there exist an action, which enables moving from one state to another. The planning problem consists in this case in finding a path connecting given node (initial state) with the other (goal state). The state space is often enormous (potentially infinite), and there are no obvious methods of conducting a search. An example of a state space for a very simple instance of a blocks world problem is given below.
