The XTT^2 Knowledge Representation
Author: Grzegorz J. Nalepa
Version: Draft 2008Q3
XTT stands for eXtended Tabular Trees.
The current version proposal XTT^2 is simply referred as XTT in this document.
It is aimed to be as the final version for the official HeKatE project (grant).
Please put bigger remarks/discussusion, to the XTT2 development page
Introduction
XTT is a knowledge representation and design formalism for rules.
It serves both as a logical and algebraic specification of rules offering a concise, transparent, and efficient with respect to density factor visual knowledge representation form.
In contrast to traditional rulebases design approaches allowing for a flat (single-level) set of rules (e.g. using the Rete-based inference engines) XTT introduces an explicit structure in the rulebase, by introducing:
tables, used to represent groups of rules working in the same context (having similar structure of preconditions),
intertable links, used to provide explicit specification of inference control, namely switching between tables, that allow for decision-tree like structure.
Each table is composed of:
its scheme or structure definition (provided within the first row of a table), and
the rules defined by the operators and values specified in the consecutive rows.
The method is used during the phase of the logical design of the rulebase. The process of defining a table covers:
identification of the operation context (informal),
definition of the scheme of a table,
filling it with appropriate relational operators and values in order to define specific rules.
XTT is a formal method based on an expressive logical calculus called Attributive Logic (or Attribute Logic).
History and Related Documents
 mscs, regulus, kheops, ijis, ecai96, oat, dexa
mscs, regulus, kheops, ijis, ecai96, oat, dexa
XTT (also referred to as XTT1) has been first formulated by Grzegorz J. Nalepa in (gjn2004phd), and later described in (gjn2005SystemScienceXTT), and gjn2005CompSciMirella.
The version described in the above papers is referred to as XTT1.
The design was supported by the Mirella tool gjn2005CompSciMirella.
An important development was the supportive design method called ARD (Attribute Relationship Diagrams).
It was first proposed by Antoni Ligeza in (ali2005thebook), and later developed by Grzegorz J. Nalepa and Antoni Ligęza in gjn2005:kkio.
In (ali2005thebook) the family of Attributive Logics (AL) including SAL (Set Attributive Logic) has been described.
Implicitly SAL was the formal foundation for XTTv1.
In the next phase of research number of possible extensions to the base XTTv1 specification has been proposed by Grzegorz J. Nalepa, Igor Wojnicki and Antoni Ligęza, for the details see:
Recently some stronger formulation for the next version of XTT have been given in:
At this stage XTT was referred to as XTT+.
The name GREP (General Rule Programming) was also proposed in gjn2007inap.
The proposal was an attempt to investigate the use of the XTT+ as a general programming solution.
Originally, for XTT1 (gjn2004phd) different conceptual design methods were considered.
The ARD method was one of the considered possibilities developed by Grzegorz J. Nalepa and Antoni Ligęza in gjn2005:kkio.
Later on it has been refactored and formally described by Grzegorz J. Nalepa and Igor Wojnicki in (gjn2007flairs-ardformal).
This current version is called ARD+.
ARD+ is the conceptual design method considered for the XTT rule design as of the HeKatE project.
However, in the future the ARD+ shall be replaced by more advanced methods.
Based on the above experiences, the current version of XTT known as XTT^2 has been proposed for the HeKatE project by Grzegorz J. Nalepa and Antoni Ligęza in 2008.
XTT^2 uses ALSV(FD) (Attributive Logic with Set Variables over Finite Domains) as the formal foundation.
Rule Attribute Specification
Rule Prototyping
In general, the logical XTT rulebase design should be preceded by a conceptual design, where certain constraints for the XTT table headers should be specified.
Currently in HeKatE the ARD+ conceptual rule prototyping method is supported.
the input of the method is the system description in the natural language
the output of the method includes:
XTT rule prototypes in a general form on conditional attributes | decision attributes
-
set of physical attributes present in rules
physical attribute specification (domains, etc.).
this specification can be provided in ARDML (HML) or in HMR (Prolog)
For more details please read the ARDplus page to fully understand the design!
XTT Constraints
Rule prototypes provide hints for XTT tables:
(Please discuss at the XTT constraints page.)
Communication Constraints
To some extent they should also point to attribute communication classes.
By default we should assume that (with respect to the system as a whole) there exists:
independent attributes (if any!) are input ones,
attributes that no other dependent on, are output ones,
attributes that are and have dependants are internal ones.
XTT Rules
On a general level, an XTT rule is a Rule of Inference or, more precisely, a production rule i.e. a basic component of any Production Rule System.
It is composed of the:
LHS (Left Hand Side), that is a set of premises, also named preconditions, specifying the condition under which it can be activated (fired), and
RHS (Right Hand Side)), that is the decision, conclusion, hypothesis or action.
Rule Prototype
The rule prototype (or scheme) is an ordered pair <P,C>, where P is a tuple of conditional attribute names, present in the premise and C is a tuple of decision attribute names.
The scheme may be precreated by the ARD+ method.
Rule LHS
The XTT rule LHS is a tuple of ALSV formulas, as described in detail in syntax.
Logically, the LHS a corresponds to a conjuction of premises (atomic formulae of the attributive logic in use) as in the classical inference rule definition.
Any rule is assumed to be of the form:
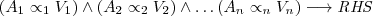 where the admissible relational symbols in ALSV(FD) are used,
and RHS is the right-hand side of the rule covering the conclusion.
where the admissible relational symbols in ALSV(FD) are used,
and RHS is the right-hand side of the rule covering the conclusion.
Rule Firing
The current values of all the attributes are specified with the contents of the knowledge-base.
From logical point of view it is a formula of the form:
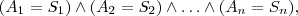 Eq: state-formula
Eq: state-formula
where
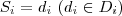 for simple attributes and
for simple attributes and
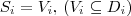 for complex ones.
for complex ones.
Having a table with defined rules the XTT inference mechanism searches for ones with satisfied preconditions.
The satisfaction of preconditions is verified in an algebraic mode, using the dependencies specified in the first row of Table 3 (see Inference rules) for simple attributes and the first row of Table 4 (see Inference rules) for the complex ones.
The rules having all the preconditions satisfied can be fired.
See Inference for more details.
Rule RHS
The XTT rule RHS is an ordered pair <D,L>,
where D is a tuple of decision formulas,
and L is a link, that is
an ordered pair <T,R>
where T and R are table and rule-in-table IDs respectivly.
The rule RHS can contain:
state changes, that is attribute values modifications (with use of retract/assert,

by iw: there is no assert/retract anymore, assuming that attributes can be multivalued, there are only set operations, an assert is represented as a sum: assert(A(1)) ⇔ A = A u {1}), possibly with use of any predefined predicates/functions etc. for now we assume all the results are explicitly represented in state!
external actions execution, that do not change attribute values, thus do not change the system state; these include output values definition and export,
link that specifies inference control (e.g. a switch/case or a loop),
Some consequences - backtracking
no parameter passing,
no backtracking,
simple solution
Attribute value modification
Attribute value modification can be done by:
1) assignement A=v where v \in D, v is a single value in case of the simple attributes, it is a set of values in case of the general attributes
2) in general 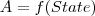 , where f(State) is
, where f(State) is
2.1) ALSV(FD) formula in case of both symbolic and numeric attributes
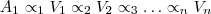 where
where 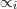 is one of the admissible relational symbols in ALSV(FD),
and the following set-theoretic operations (see Algebra of Sets:
union, intersection, difference (relative complementation), complementation (absolute complementation to the domain).
and V is a named set of values, or another attribute reference.
is one of the admissible relational symbols in ALSV(FD),
and the following set-theoretic operations (see Algebra of Sets:
union, intersection, difference (relative complementation), complementation (absolute complementation to the domain).
and V is a named set of values, or another attribute reference.
2.2) Algebraic expressions in case of numeric attributes only; the expression can contain numbers, predefined algebraic operators and functions/predicates, as well as attribute values (Prolog is).
3) External action specification;
it contains a single predicate call, that possibly uses any attributes present in the table header as arguments.
Warning: see Inference Constraints.
In the value modification only attributes present in the given table may be used!
 do we need anything else as of using ALSV+ST relations to modify value? check if all alsv symbols apply!
do we need anything else as of using ALSV+ST relations to modify value? check if all alsv symbols apply!
(Please discuss at the Attribute value modification page.)
Tables
XTT rules are combined into attributive decision tables,
grouping rules having the same prototypes, that is having the same conditional and decision attributes.
XTT table is composed of rows, that correspond to rules.
Columns group formulas having the same attribute.
Cells can be interpreted as formulas in given rules at a given position.
A XTT cell corresponds to an atomic formula in ALSV(FD),
that is, it is a triple in the form of A R V, where
A is attribute name
for simple attributes R is one of: eq, neq, in, notin
for general attributes R is one of: eq, neq, subset, supset, sim, notsim
V is the (multi)value to compare with.
A table provides a visual representation of rules, as below.


Rules in the table are interpreted one by one in a given way (see Inference), this is the Table Inference.
Table rows (rules) may be connected to other tables (rows) by links.
This forms a tree-like structure.
This is the Tree-like Inference.
(In fact, it is more close to a graph representing a partial order of inference).
Table Scheme
XTT tables group rules with exactly the same schemes or prototypes.
This is why the table scheme (or header, prototype) is exactly the same as the rule prototype.
Table Types
In order to simplify both the design and formal analysis certain types of tables are considered.
 In the future more types could be identified.
(Please discuss at the Table types page.)
In the future more types could be identified.
(Please discuss at the Table types page.)
It seems that we should consider also:
input or set of input cases to be processed (states),
functional calculation i.e. a table performing any well-defined calculation,.
This should be reconsidered with the above material on Rule RHS.
Inference
Rules are grouped into tables, depending on their attributes.
Tables can be linked (row or table level).
Link interpretation is:
context change
inference control
process model
partial order
This makes up a decision-tree like structure, with tables in the tree nodes.
In a general case, the XTT is a directed graph, with cycles optionally allowed.
Table inference
In general, rules can be fired in parallel (at least in theory) or sequentially.
For the following analysis we assume the classical, sequential model, i.e. the rules are examined in turn in the top-down order and fired if the preconditions are satisfied.
Various mechanisms can be used to provide a finer inference control mechanism.
Propagation Mechanism
In order to avoid repeated checking of preconditions a propagation mechanism is proposed for satisfaction and falsification of atomic formula within the table.
Let c(i,j) denote the atomic formula related to the cell located in row i and column j.
The idea can be summarized as follows:
once the table is defined it is searched top-down (off-line) for establishing dependencies between any atomic cell c(i,j) of rule i and all the cells c(k,j) (in the same column) of any rule k, where k>i;
in case some two cells c(i,j), c(k,j) satisfy a condition of logical consequence as specified in Table 3, a positive link p(i,k,j) is established; all the links are kept in memory; in case some two cells c(i,j), c(k,j) satisfy a condition of logical inconsistency as specified in Table 4, a negative link n(i,k,j) is established; all the links are kept in memory;
during execution phase, if a cell c(i,j) is checked and the related atomic formula is satisfied, the truth value is propagated for the transitive closure defined with use of the positive links; the respective atoms are marked true and do not need to be checked in this turn;
during execution phase, if a cell c(i,j) is checked and the related atomic formula is true, the false value is propagated for the transitive closure defined with use of the negative links; the respective atoms are marked false and the corresponding rules are eliminated from this cycle.
This mechanism saves computational effort corresponding to repeated precondition checking and saves time in case some preconditions are logically dependent (one is logical consequence of the other or they are mutually exclusive).
 In fact this can be made even more general:
In fact this can be made even more general:
This is to be reexamined and restated; a comparison to Rete may be in order.
Tree inference
XTT tables are connected with links.
A link represents a inference control mechanism.
It also be thought of as a
dependency mechanism,
context change,
process model,
partial order.
Links are deterministic, that is a single rule decision can have a single link only.
In general we consider positive links, that is links that are followed where a rule is fired.
The designer can introduce explicit negative links by
using an explicitly defined positive construction of the following scheme:
precondtions --> conclusion| next(table.rule)
true --> | else(table.rule)
 We can consider introducing number of global meta-interference attributes,
such as “mode_of_operation”, “task”, “did_any_rule_in_table_fired”, etc.
We can consider introducing number of global meta-interference attributes,
such as “mode_of_operation”, “task”, “did_any_rule_in_table_fired”, etc.
Links
In general, the following link classes are considered:
rule-table (r2t) a given rule in a given table when fired, transfers control to another table, meaning the inference starts at the first rule of the destination table. This is considered the default for XTT^2.
rule-rule (r2r) a given rule in a given table when fired, transfers control to another rule in another table, or possibly the same table (inside table link.
 : iw: I'm still not convinced about rule-rule links, any advantages? There are some disadvantages though, ie: if we change the rule firing order (let's say bottom-up instead of top-down,) rule-rule links can screw us really bad. Having rule-table links only forces designer to come up with well designed conditions. So, because there are some doubts I would recommend not implementing it for time being at all.
: iw: I'm still not convinced about rule-rule links, any advantages? There are some disadvantages though, ie: if we change the rule firing order (let's say bottom-up instead of top-down,) rule-rule links can screw us really bad. Having rule-table links only forces designer to come up with well designed conditions. So, because there are some doubts I would recommend not implementing it for time being at all.
More on intertable links
In general, we should have inter-tables links and inside-table links.
Both of them can be defined with TableOut.RuleOut –> TableIN.RuleIN model.
However, for the inside table links we can define simple policies, such as a top-bottom order, top-first-fired order, without without circular interpretation.
Link implementation
links can be encoded as a pair of outgoing/destination table/rule id at the rule level.
they can represented in the Prolog rule base by the xtt_link/3 predicate, having source, and destination IDs, with some optional link comment/label etc. This could be the base or additional representation to the first one.
Using the 2nd solution it would be easy to find all tables/rules on which a given rule/table depend by backward chaining.
Branching
Problem: In a general case, there might be multiple entry points in the XTT structure.
(See the discussion at the Branching page.)
A temporary semi-parallel solution:
ARD introduces partial order in tables,
tables can be fired in any way,
as long as this contstraint holds.
 : iw: not really there might be more than one table with input attributes (or ro, rw) in the condition parts, it might be not doable to infer which table should be run first.
There might be an algorithm implemented which finds an order of execution (which table to start with), but any conditions using a N/D value can screw it.
I'd suggest choosing an entry table, the one that the inference process starts with, explicitly.
: iw: not really there might be more than one table with input attributes (or ro, rw) in the condition parts, it might be not doable to infer which table should be run first.
There might be an algorithm implemented which finds an order of execution (which table to start with), but any conditions using a N/D value can screw it.
I'd suggest choosing an entry table, the one that the inference process starts with, explicitly.
Interpreter Scenarios
The XTT logic is a knowledge base executed by an inference enngine, that is the XTT rule metinterpreter, also known in HeKatE as HeaRT.
HeaRT
Some of the most basic interpreter functions are:
-
analyze XTT rules in XTT tables,
provide inference control by interpreting links,
manage the attributes by the
Blackboard Architecture, by synchronizing attribute values between the system and the environment,
Extended functions, provide:
on-line formal verification capabilities,
on-line refinement of the XTT rule-base,
a bridge to HQed,
OO bridge to Java in MVC, where HeaRT is the M, Java provides V, consider different approaches to C
a bridge to ANSI C
standalone logic server with TCP
dynamic logic serialization to Java and C
Advanced
Several interpreter types, or use scenarios are considered.
These scenarios try to address issues such as when and how and how many times is the interpreter run.
Currently only the simplest one is described.
Single Pass
The Single Pass interpreter is the simplest scenario:
the interpreter is executed externally by the user, system, etc.
input attribute callbacks provide input facts
the inference starts
-
links are followed
inference process ends
output attribute values can be sent by callbacks
For sanity, it should be assumed, that no attributes input/communication attributes are updated during the inference.
 Here we can think about a transaction-like mode and possible attribute freezing or more lively models. Various possibilities of separation both among tables and tables vs. environment can be considered.
Here we can think about a transaction-like mode and possible attribute freezing or more lively models. Various possibilities of separation both among tables and tables vs. environment can be considered.
This is the basic mode, that should be considered, implemented, and analyzed before any other options.
For other modes see Interpreter Scenarios.
System Communication
State Modeling
The following assumptions for system modeling with ALSV rules is given:
the system is modeled with the use of attributes (state variables!),
the state of the system is fully described with attribute values,
rule firing can possibly change system state by changing attribute values,
rules can execute actions external to the system,
it is assumed that these actions do not change system state,
the state can be changed from the outside.
Perspectives:
It could be summarized, that “communication” between the system and the world is conducted using attributes and their values.
Blackboard Architecture
Attributes are considered shared resources.
The XTT logic can access the attribute values in the XTT tables.
The values can be accessed from the outside of the system/interpreter (from the environment).
The values are modified/updated by both the environment and the system simultaneously.
A simple locking/semaphore approach is exercised.
This approach should be independent of the intepreter scenarios!
The access and update policy depends on the attribute class.
Attributes Classes
Several attribute classes are considered:
Arrows indicate the System/Environment interaction.
 : iw: what's happened to
: iw: what's happened to ro, rw, wo, state classes?
Discuss ideas here: Attribute Classes.
Attribute Callbacks
The actual value modification is provided by a middle layer of attribute callbacks.
For now it is assumed that a callback is a predicate run by the intepreter to pull (input) or push (output) attribute values.
If an asynchronous interpreter mode is considered attribute locking should be provided during update.
During the implementation discuss experiences here: Attribute Callbacks.
The following textual algebraic representation is provided.
It is to be generated by the design tool (e.g. HQed) and directly run by HeaRT.
Table scheme, logically also rule prototype.
xttscheme:
[a1,...,an],
[h1,...,hm].
Rule:
xttrule: [Table, Id]:
[c1,...,cn]
then
[d1,...,dn],
[Table, Id].
Fact:
XTT Analysis

XTT on ALSV allows for a formal analysis of important system properties during the logical design, e.g.:
consistency, and
completeness
Appropriate algorithms for XTT^2 should be developed.
In general, there are at least the follwoing possibilities:
rule-rule (pairwise) analysis (e.g. identical rules, subsumption, exclusive rules - determinism),
rules-in-table (all) analysis (e.g. local, contextual completeness, determinism),
chains-of tables/rules analysis (unprovided facts, unused conditions, unreachable conclusions, etc.).
Further, any path should be analyzed for calculability or executability, i.e. if it can be followd (no part of information is missing) and – if parallel action are allowed – for determinism and deadlocks.
XTT^2 Markup
SPOOL
see for  s in this page.
s in this page.
Constraints from ARD
XTT^2 Features Summarized
Selected:

Rule Examples
XTT^2 Optional Extensions
Possible
Inference with backtracking and cut
Hierarchical types
hierarchical types, e.g. temp1 is a the same as temp but with restricted range
is this too redundant?
XTT Blocks
Blocks, as simulink boxes to simplify the design.
This could be possibly cobmined with the so-called scope from the XTT+.
Link labeling
Deprecated
direct AVR

grouped atts
hybrid opps
Pending and Future Work
BPMN
From XTT to BPMN and back again
DICS
declarative inference control spec
 This perhaps we should leave as a research thread only.
This perhaps we should leave as a research thread only.
Fixed, simple declaration of control inference (with a few parameters only + the links) should be sufficient to demonstrate the power of XTT!
On the other hand we have to re-think the problems and advanatges of using cut (!) and similar mechanism (e.g. fail, exit).
 mscs, regulus, kheops, ijis, ecai96, oat, dexa
mscs, regulus, kheops, ijis, ecai96, oat, dexa
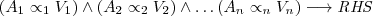 where the admissible relational symbols in ALSV(FD) are used,
and RHS is the right-hand side of the rule covering the conclusion.
where the admissible relational symbols in ALSV(FD) are used,
and RHS is the right-hand side of the rule covering the conclusion.
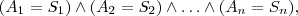 Eq: state-formula
Eq: state-formula
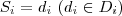 for simple attributes and
for simple attributes and
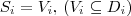 for complex ones.
for complex ones.
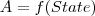 , where f(State) is
, where f(State) is
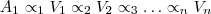 where
where 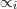 is one of the admissible relational symbols in ALSV(FD),
and the following set-theoretic operations (see
is one of the admissible relational symbols in ALSV(FD),
and the following set-theoretic operations (see 
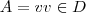 are allowed in the decision, actions are also allowed (they do not change state)
are allowed in the decision, actions are also allowed (they do not change state)