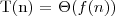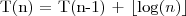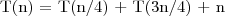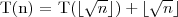Złożoność algorytmów
Termin zajęć: 29/30.03.2011
Do przygotowania:
Znajomość i rozumienie pojęć:
Złożoność obliczeniowa.
Złożoność pamięciowa:
Działanie algorytmów „w miejscu”.
Złożoność pesymistyczna.
Złożoność oczekiwana.
Złożoność optymistyczna.
Zajęcia odbywać się będą głownie przy tablicy.
Nie ma konieczności przynoszenia laptopów.
Metoda rekurencji uniwersalnej
Umożliwia szybkie wyznaczanie rozwiązania równania rekurencyjnego postaci:
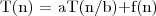 gdzie:
gdzie:
Wtedy T(n) może być ograniczona asymptotycznie w następujący sposób:
Jeżeli
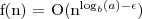
dla pewnej stałej ε > 0 to,
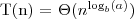
Jeśli
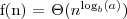
to,
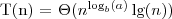
Jeżeli
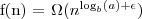
dla pewnej stałej ε > 0 oraz
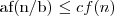
dla pewnej stałej
c i wszystkich dostatecznie dużych
n, to
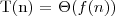
Zadania
Metodą reukrencji uniwersalnej wyznacz złożoność obliczeniową algorytmu wyszukiwania binarnego.
Rozwiąż w sensie asymptotycznym następujące równanie rekurencyjne:
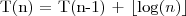
Rozwiąż w sensie asymptotycznym następujące równanie rekurencyjne:
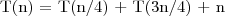
Rozwiąż w sensie asymptotycznym następujące równanie rekurencyjne:
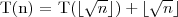
Niejasności z zajęć
Metoda graficzna:
for(i=0;i<n;i++)
for(j=0;j<n;j++)
OD
for(i=0;i<n;i++)
for(j=0;j<n;j+=2)
OD
i(n)=n
j(i)=n/2
T(n)=n^2/2
for(i=0;i<n;i+=2)
for(j=0;j<i;j++)
OD
i(n)=n/2
j(i)=i
T(n)=n^2/8
for(i=0;i<n;i+=2)
for(j=i;j>=1;j/=2)
OD
i(n)=n/2
j(i)=log i
T(n)=n/2(log(n/2) - 1)
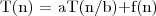 gdzie:
gdzie:
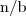 interpretujemy jako
interpretujemy jako 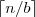 lub jako
lub jako 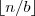
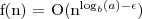 dla pewnej stałej ε > 0 to,
dla pewnej stałej ε > 0 to, 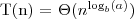
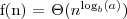 to,
to, 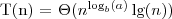
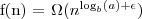 dla pewnej stałej ε > 0 oraz
dla pewnej stałej ε > 0 oraz 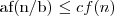 dla pewnej stałej c i wszystkich dostatecznie dużych n, to
dla pewnej stałej c i wszystkich dostatecznie dużych n, to