Modelowanie gier w GDL
Celem laboratorium jest zrozumienie regułowego opisu gier turowych. Student po zakończeniu laboratorium powinien potrafić zamodelować proste gry oraz wskazać trudności związane z tym zadaniem.
1 Preliminaria
GDL (Game Description Language) jest językiem opisu gier turowych. Powstał na potrzeby General Game Playing - działu sztucznej inteligencji, który zajmuje się szukaniem strategii grania, które działałyby niezależnie od zasad gry. Innymi słowy, bot powinien być w stanie grać (i wygrać) w dowolną grę opisaną w języku GDL.
Laboratoria bazują w dużej mierze na tutorialu ze Stanfordu oraz slajdach z uniwersytetu z Dresden.
2 Modelowania świata gry
Istnieją dwa zasadnicze podejścia do modelowania świata/środowiska gry. Jedno z nich (nazwijmy je gruboziarnistym) traktuje świat jako maszynę stanową - gdzie każdy unikalny stan świata jest reprezentowany jako oddzielny stan maszyny. Unikalność stanu traktujemy tu na poważnie, co do jednego zaplutego, spróchniałego pnia, zatem można się domyślić, że maszyna stanowa nawet dla prostych gier będzie ogromna. Poza tym stan jest czymś pozbawionym struktury, co nie pomaga w inteligentnym rozwiązywaniu problemu.
Z drugiej strony mamy języki w stylu PDDL, które dynamikę świata modelują przy użyciu fluentów - zdań logicznych, które zmieniają wartość. Tutaj stan świata ma strukturę (aktualne wartościowanie fluentów), które można wykorzystać podczas planowania, wnioskowania, etc.
GDL należy do drugiego podejścia - stan gry modelowany jest poprzez fluenty. Poza nimi w skład gry wchodzą akcje graczy (również modelowane w postaci fluentów) oraz reguły gry, które są reprezentowane w postaci… reguł.
3 Przykład: Kółko i krzyżyk
Gracze
Zacznijmy od tego, że w grze występuje dwóch graczy o pięknych imionach „kolko” i „krzyzyk”. Służy do tego predefiniowany fakt role:
Składnia jest taka sama jak w języku Prolog (lub Datalog) z tą różnicą, że na końcu nie ma kropki. Ponownie stałe pisane są małą, a zmienne wielką literą.
Definiowanie fluentów
Następnie należy zdefiniować fluenty, które będą opisywać stan gry. W przypadku kółka i krzyżyk stan gry opisany jest przy pomocy 29 fluentów:
po 1 fluencie na każdą komórkę, mówiącym, czy w tej komórce jest krzyżyk (razem 9 fluentów)
po 1 fluencie na każdą komórkę, mówiącym, czy w tej komórce jest kółko (razem 9 fluentów)
po 1 fluencie na każdą komórkę, mówiącym, czy ta komórka jest pusta (razem 9 fluentów)
po 1 fluencie na każdego gracza, mówiącym, czy to jest tura danego gracza (razem 2 fluenty).
W celu zdefiniowania fluentów należy się posłużyć predefiniowanym predykatem base:
Symbol :- to podobnie jak w Prologu implikacja ←. & reprezentuje koniunkcję. W języku naturalnym można powiedzieć, że pierwsza linijka powyższego kodu oznacza: „jeżeli M i N to prawidłowe indeksy komórki, to istnieje fluent dla komórki o współrzędnych M i N, mówiący o tym, że jest w niej krzyżyk”. Bez użycia reguł musielibyśmy wszystkie fluenty definiować wprost:
Reguły w GDL'u różnią się od reguł Prologowych pod jednym ważnym aspektem: musi być zapewniony fakt, że się nie zapętlą. Więcej szczegółów na ten temat w slajdach z uniwersytetu z Dresden.
Dostępne akcje
Teraz należy się zastanowić nad tym, jakie akcje są wykonywalne w grze. W przypadku kółka i krzyżyk jest ich 20:
1 akcja dla każdej komórki, mówiąca, że gracz 'kółko' ją zaznacza (łącznie 9)
1 akcja dla każdej komórki, mówiąca, że gracz 'krzyżyk' ją zaznacza (łącznie 9)
1 akcja noop dla każdego grazca, mówiąca, że gracz nie wykonał ruchu (łącznie 2).
Akcja noop istnieje tylko po to, żeby zasymulować odpowiednio ruchy graczy na zmianę. Gracz w nie swojej turze może jedynie wykonać noop.
W celu zdefiniowania akcji posługujemy się wbudowanym predykatem input:
Predykat input przyjmuje dwa argumenty, pierwszy to nazwa gracza, który może wykonać akcję, drugim jest sama akcja.
Dozwolone ruchy
Teraz, znając już możliwe akcje, wypadałoby powiedzieć, kiedy dany ruch jest dozwolony. Służy do tego predykat legal. Aby sprawdzić, czy dany fluent jest aktualnie prawdziwy posługujemy się predykatem true.
legal(W,mark(X,Y)) :-
true(cell(X,Y,b)) &
true(control(W))
legal(kolko,noop) :-
true(control(krzyzyk))
legal(krzyzyk,noop) :-
true(control(kolko))
Innymi słowy - gracz może zaznaczyć dane pole, o ile jest puste i jest jego tura. Gracz może też wykonać akcję noop, jeżeli tura należy do przeciwnika.
Stan początkowy
Podobnie jak w PDDL'u, musimy zdefiniować stan początkowy świata. Służy do tego tego predykat init. Możemy przy jego pomocy określić, które fluenty są prawdziwe u zarania dziejów. Dla kółka i krzyżyk, wszystkie komórki są puste, a tura należy do kółka:
Zmiana stanu
Teraz przechodzimy do części najtrudniejszej — w jaki sposób zamodelować zmiany stanu świata. Zakładamy, że czas w grze jest dyskretny i w każdej kolejnej turze gry obliczany jest nowy stan świata. Zależy on jedynie od poprzedniego stanu świata oraz akcji wykonanych przez graczy. Pojawia się tutaj problem ramki (lub klatki). Nazwa pochodzi od analogii między następującymi po sobie stanami świata z klatkami na taśmie filmowej. Wszystkie klatki filmowe są od siebie niezależne, różnią się od swoich poprzedników jedynie szczegółami — reszta jest taka sama. Podobnie tutaj chcielibyśmy, żeby poza explicite zamodelowanymi zmianami, reszta świata pozostała bez zmian. W naszym przypadku oznacza to, że musimy zamodelować również brak zmiany 
Do definicji reguł zmiany stany w GDL posługujemy się predykatem next, mówiącym, czy fluent będzie prawdziwy w kolejnej turze. Predykat 'does' pozwala na sprawdzenie, jaką akcję dany gracz wykonał w aktualnej turze:
Akcje te kolejno oznaczają:
jeżeli komórka jest pusta, a gracz krzyżyk ją zaznaczył, to w kolejnej turze w tej komórce będzie krzyżyk
jeżeli komórka jest pusta, a gracz kółko ją zaznaczył, to w kolejnej turze w tej komórce będzie kółko
jeżeli dana komórka nie była pusta (pomocniczy predykat distinct sprawdza tożsamość argumentów), to w kolejnej turze będzie miała te samą zawartość
jeżeli dana komórka była pusta, ale nie była komórką, która została zaznaczona, to w kolejnej turze też będzie pusta (aż dwie reguły!)
jeżeli dana tura należała do kółka, to kolejna będzie należała do krzyżyka
jeżeli dana tura należała do krzyżyka, to kolejna będzie należała do kółka
Warto zauważyć, że akcje 3 i 4 służą właśnie walce z problemem ramki.
Warunki końca gry
Każdy wie, że celem gry w kółko i krzyżyk jest ułożenie linii. Żeby sprawdzić, czy w danym stanie ułożona jest linia, należy zdefiniować odpowiednie reguły:
Zapytanie true(line(kolko)) powie nam teraz, czy na planszy jest linia kółek.
Teraz należy zdefiniować kryteria zakończenia gry, używając predykatu terminal:
Gra się kończy, gdy:
istnieje linia krzyżyków
istnieje linia kółek
wszystkie pola są zajęte
Operator '~' oznacza negację. Podobnie jak w prologu działa ona na zasadzie świata zamkniętego, tzn. zdanie uznajemy za fałszywe, jeżeli nie potrafimy udowodnić, że jest inaczej. W GDL'u istnieją specjalne obostrzenie ograniczające stosowanie negacji, ale na razie nie musimy się tym przejmować (więcej info na slajdach z uniwersytetu z Dresden).
Kryterium zwycięstwa
 Koniec zabawy — boty nie mają uczuć, nie mogą więc czerpać z gry przyjemności. Natomiast nadal mogą dostawać nagrody za dobrą grę. I naszym obowiązkiem jest te nagrody rozdać. W tym celu posługujemy się predykatem
Koniec zabawy — boty nie mają uczuć, nie mogą więc czerpać z gry przyjemności. Natomiast nadal mogą dostawać nagrody za dobrą grę. I naszym obowiązkiem jest te nagrody rozdać. W tym celu posługujemy się predykatem goal:
Powyższe reguły mówią, że w przypadku zwycięstwa gracz dostaje całe 100 (tyle wygrać!), w przypadku remisu 50, a w przypadki porażki 0. Nie wiemy, co ta liczba symbolizuje, ale uznajmy, że są to ciasteczka, albo coś, czego nigdy nie za wiele.
W GDL nie ma arytmetyki — liczby nie różnią się niczym od innych stałych. Stosowane są głównie do zliczania kroków oraz rozdawania nagród.
Koniec
To by było na tyle, właśnie udało się zamodelować prostą grę w kółko i krzyżyk.
3.1 Zad 1
Weźmy przykładowy model jeszcze prostszej gry.
Odpowiedz na poniższe pytania:
jak wielu graczy występuje w grze?
jak wiele fluentów opisuje stan gry?
jak wiele jest dostępnych akcji?
ile akcji może wykonać gracz 'white' w początkowym stanie gry?
jak wiele fluentów jest prawdziwych w początkowym stanie gry?
załóżmy, że pierwszej turze gracz 'white' wykonał akcję 'a', a gracz 'black' akcję 'd'. Ile fluentów jest prawdziwych w drugiej turze?
jaka jest najmniejsza liczba kroków potrzebna do zakończenia gry?
czy gra zawsze się kończy? (czy mogłaby się zapętlić?)
3.2 Zad 2
Proszę zamodelować grę w 'krzyżyk i krzyżyk'. Podobnie jak w przypadku 'kółka i krzyżyk' mamy dziewięć pól, tym razem jednak obaj gracze stawiają krzyżyki. Przegrywa ten gracz, który pierwszy doprowadzi do powstania linii.
3.3 Zad 3
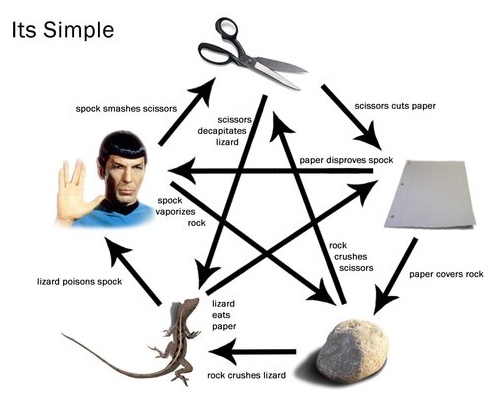 Proszę zamodelować grę w „kamień, papier, nożyce, spocka i jaszczurkę”. W razie problemów ze zrozumieniem reguł, proszę obejrzeć instrukcję video. Obrazek obok przedstawia użyteczną referencję. . Poćwiczyć można na żywo w sali, lub, jak na prawdziwego człowieka XXI wieku przystało, online....
Proszę zamodelować grę w „kamień, papier, nożyce, spocka i jaszczurkę”. W razie problemów ze zrozumieniem reguł, proszę obejrzeć instrukcję video. Obrazek obok przedstawia użyteczną referencję. . Poćwiczyć można na żywo w sali, lub, jak na prawdziwego człowieka XXI wieku przystało, online....
O ile wszystko, co zostało powyżej napisane, jest prawdą, o tyle większość systemów GGP nie wspiera reprezentacji w stylu Prolog. Na potrzeby wysyłania i zapisania wiedzy (reprezentowanej w sposób regułowy) powstał format KIF (Knowledge Interchange Format). Podobnie jak w przypadku PDDL, bazuje on na lispie i używa notacji prefixowej. Ponadto symbol :- zestępowany jest przez strzałkę ⇐, symbol koniunkcji & przez and, symbol negacji ~ przez not. Nazwy zmiennych poprzedzane są znakiem zapytania ?. Poniżej przedstawiony jest przykład translacji z wersji a'la Prolog:
do formatu KIF:
4.1 Zad 1
Dla każdej z poniższych par określ, czy wersja prefixowa, jest wiernym tłumaczeniem wersji Prologowej.
4.2 Zad 2
4.3 Zad 3
4.4 Zad 4
Przepisz modele 'kólka i krzyżyka', 'krzyżyka i krzyżyka' oraz 'papier, kamień, nożyce, spocka i jaszczurki' do postaci KIF.
5 Walidacja modeli
Poniższe instrukcje przygotowane są z myślą o laboratorium C2 316, gdzie każdy komputer ma Eclipse.
Proszę uruchomić Eclipse i następnie:
File → Import Project
Wybrać opcję importowania z repozytorium git
Jeżeli tej opcji nie ma (Eclipse jest za stare), to trzeba ręcznie sklonować repo i zaimportować projekt z katalogu. Reszta tutejszej instrukcji nie ma sensu

Wybrać opcję klonowania z zewnętrznego
URI-
Wybrać gałąź master
Wybrać jakiś rozsądny katalog dla projektu
Wybrać projekt ggp-base do zaimportowania
5.1 Dodanie gier do środowiska
W katalogu projektu proszę dostać się do ścieżki games/games i stworzyć tam trzy katalogi kolko-krzyzyk, krzyzyk-krzyzyk i spock. Każdy katalog powinien zawierać dwa pliki:
5.2 Walidacja gier
Z poziomu Eclipse proszę uruchomić aplikację Validator (rozwijana lista przy guziki play).
Validator, jak sama nazwa wskazuje, ma na celu sprawdzenie, czy dany model jest prawidłowym modelem GDL.
Ćwiczenia
W polu Repository wybrać Local Game Repository
W polu Game wybrać Tic-Tac-Toe
Wciśnąć przycisk Validate — program powinien pokazać same sukcesy
Powtórzyć to samo dla własnych modeli
Poprawić własne modele
Zdobyć kolejne sukcesy.
6 Zabawa
Z poziomu Eclipse proszę uruchomić aplikację Kiosk (rozwijana lista przy guziki play).
Ćwiczenia
W polu Opponent proszę wybrać SimpleMonteCarloPlayer
Wybrać jakąś znajomą grę
Wygrać!




