KRR: Logiki Deskrypcyjne - odpowiedzi
Wprowadzenie
Pojęcia (klasy):
cat_liker, cow, man, cat, vegetarian, person, sheep, adult, male, animal, grass
Role (relacje):
has pet, is a, is an, likes, doesn't eat, eats only
Instancje (obiekty):
Fred, Tibbs
Reprezentacja - zadanie
-
Opisy i ich rozszerzenia w interpretacji:
(∃ areMarried.Doctor ⊓ (∃ hasPet.Dog))^I = {Suzan};
(∀ areFriends
1)) ⊓ ¬∃ areMarried.⊤)^I = {Max,Helen,Nick}
Aksjomaty i ich rozszerzenia:
¬∃ areFriends.Male ⊑ ¬hasPet.⊤
nieprawdziwe przy danej interpretacji.
ponieważ: (¬∃areFriends.Male)I = {John, Suzan, Helen, Max, Nick}; (¬hasPet)I = {Helen, Max, Natalie, Nick}, i pierwszy zbiór nie jest podzbiorem drugiego
ponieważ Susan nie ma męskich przyjaciół, a ma zwierzę.
Male ⊑ (∃ areMarried.⊤) ⊔ ∃ areFriends.¬Male.
nieprawdziwe przy danej interpretacji.
ponieważ rozszerzenie lewej strony to: {Max, John, Nick} a prawej: {John, Suzan} ∪ {Nick, Helen, Suzan, Natalie} i pierwszy zbiór nie jest podzbiorem drugiego.
ponieważ Max jest rodzaju męskiego, a nie jest ani w związku małżeńskim ani nie ma przyjaciół.
Poniższe zdania przełożono z języka naturalnego na formuły rachunku pierwszego rzędu.
Dopisz odpowiadające im zdania w logice deskrypcyjnej.
Każdy ogrodnik lubi słońce. / Every gardener likes the sun.
(Ax) Gardener(x) ⇒ likes(x,Sun)
-
Niektórych ludzi możesz nabrać zawsze. / You can fool some of the people all of the time.
(Ex) (person(x) ^ (At)(time(t) ⇒ can-fool(x,t)))
-
Czasami możesz nabrać wszystkich ludzi. / You can fool all of the people some of the time.
(Ax) (person(x) ⇒ (Et) (time(t) ^ can-fool(x,t)))
-
Wszystkie fioletowe grzyby są trujące. / All purple mushrooms are poisonous.
(Ax) (mushroom(x) ^ purple(x)) ⇒ poisonous(x)
-
Żadne fioletowe grzyby nie są trujące. / No purple mushroom is poisonous.
~(Ex) purple(x) ^ mushroom(x) ^ poisonous(x)
(Ax) (mushroom(x) ^ purple(x)) ⇒ ~poisonous(x)
-
Deb nie jest wysoka. / Deb is not tall.
~tall(Deb)
-
TBox
∃ prowadzi.Przedmiot ⊑ ∃ maTytuł.Mgr ⊔ Wykładowca
Wykładowca ⊑ ∃ prowadzi.Przedmiot
Wykładowca ⊑ ∃ maTytuł.Inż
∃ maTytuł.Mgr ⊑ ∃ maTytuł.Inż
ABox
relacje: friend, loves
klasy: Female
obiekty: john, susan, andrea, bill
graf:
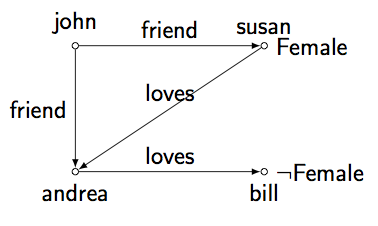
john : ∃friend.(Female ⊓ ∃loves.¬Female)
Wnioskowanie
TBox:
Pojęciu pustemu (
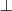
), czyli jest to pojęcie sprzeczne.
Tak, to zdanie jest logiczną konsekwencją zadanej bazy wiedzy, ponieważ:
na podstawie
1. aksjomatu każdy kto prowadzi przedmiot musi mieć albo tytuł mgr albo być wykładowcą.
jeżeli ma tytuł Mgr, to na podstawie
4. aksjomatu ma też tytuł Inż.
jeżeli jest wykładowcą to na podstawie
3. aksjomatu ma tytuł Inż.
zatem każdy kto prowadzi przemiot ma tytuł inzyniera.
ABox:
Tak, ponieważ każda starsza pani musi mieć jakieś zwierzę, a jednocześnie wszystkie jej zwierzęta to koty.
Starsza pani.
Kot.
Rozważamy następujący świat:

,
w którym nie wiemy, czy andrea jest kobietą czy nie. Rozważamy zatem dwie interpretacje:
Andrea należy do klasy Female: Wtedy Andrea jest przyjaciółką Johna i kocha Billa, który nie jest kobietą. → ✔
Andrea należy do klasy ¬Female: Wtedy Susan jest przyjaciółką Johna i kocha Andrea, który nie jest kobietą. → ✔



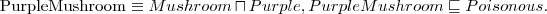
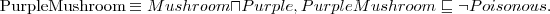
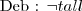

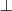 ), czyli jest to pojęcie sprzeczne.
), czyli jest to pojęcie sprzeczne.