Wnioskowanie w logikach deskrypcyjnych
Logiki opisowe, dzięki formalnemu ugruntowaniu w logice, umożliwiają automatyczne wnioskowanie.
Osobne zadania wnioskowania definiuje się dla TBoxa i ABoxa.
-
Podstawowymi algorytmami dla DL są:
Złożoność obliczeniona poszczególnyc zadań wnioskowania zależy od siły ekspresji języka DL

1 Zadania wnioskowania dla TBoxa
Spełnialność (ang. satisfiability)
Pojęcie C jest
spełnialne względem terminologii T jeżeli istnieje model (interpretacja) I taki że
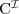
jest niepusty.
Subsumcja
1) (ang.
subsumption)
Pojęcie C jest włączone w pojęcie D wzg. T jeżeli
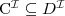
dla każdego modelu I terminologii T.
Równoważność (ang. equivalence)
Dwa pojęcia C i D są sobie
równoważne wzg. T jeżeli

dla każdego modelu I terminologii T.
Rozłączność (ang. disjointness)
Dwa pojęcia C i D są
rozłączne wzg. T. jeżeli
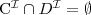
dla każdego modelu I terminologii T.
Ćwiczenie 6
Wiedząc, że:
-
-
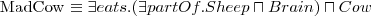
Odpowiedz na pytanie:
Jakiemu pojęciu jest równoważne pojęcie MadCow?
-
Czy zdanie„ „Każdy kto prowadzi przedmiot musi mieć tytuł inżyniera” jest logiczną konsekwencją tej bazy wiedzy? Odpowiedź uzasadnij.
2 Zadania wnioskowania dla ABoxa
Sprawdzenie spójności (ang. consistency checking)
Sprawdzanie instancji (ang. instance checking)
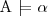
iff każda interpretacja spełniająca A spełnia również α.
Poszukiwanie najbardziej szegółowego pojęcia dla danej instancji (ang. realization).
Poszukiwanie instancji danego pojęcia (ang. retrieval).
Uwaga:
Ćwiczenie 7:
Wiedząc, że:
Czy każda starsza pani musi mieć kota? Dlaczego?
Do jakiej klasy należy obiekt Minnie?
Do jakiej klasy należy obiekt Tom?
Rozważ opis świata z sekcji
abox i odpowiedz na pytanie:
Odpowiedzi: wnioskowanie
3 Założenie o otwartości świata
Analogia bazy wiedzy DL i relacyjnej bazy danych:
W przeciwieństwie do relacyjnych baz danych, brak w ABox oznacza brak wiedzy, nie zaś negatywnąinformację
ABox reprezentuje potencjalnie nieskończenie wiele interpretacji.
Semantyka otwartego świata wymaga nietrywialnych mechanizmów wnioskowania, a realizaja zapytań jest bardziej skomplikowana.
BONUS:
4 Algorytmy wnioskowania
Strukturalne
Porównują strukturę składniową pojęć.
Są efektywne, ale odpowiednie tylko do prostych języków, np. nie działają dla języków z negacją i dysjunkcją
Tableau
Opierają swoje działanie na obserwacji, że: 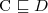 wtw. gdy wyrażenie
wtw. gdy wyrażenie 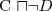 jest niespełnialne.
Schemat działania:
jest niespełnialne.
Schemat działania:
Start od faktów (aksjomatów ABox)
Doprowadzenie do normalnej formy negacyjnej (NNF). Jest to forma, w której negacja występuje tylko przd nazwami klas.
Dekompozycja składniowa z użyciem odpowiednich reguł tzw. tableaux expansion rules
Wnioskowanie o ograniczeniach na elementach modelu
Stop, kiedy nie można zastosować więcej reguł lub wystąpiła sprzeczność
Proszę zapoznać się szczegółowo z trzema przykładami z ze slajdów. Proszę przeczytać strony 22-30.
Ćwiczenie 8 (dla chętnych):
Sprawdź czy poniższe pojęcia są spełnialne:
A ⊓ ∃R.C ⊓ ∀R.D
∃R.C ⊓ ∀R.¬(C ⊓ D)
A⊓∃R.C⊓∀R.D⊓∀R.¬(C⊓D)
∃R.(A ⊓ ∃R.C) ⊓ ∀R.¬C
∃R.(A ⊓ ∃R.C) ⊓ ∀R.∀R.¬C
¬C ⊓ ∃R.C ⊓ ∀R.(¬C ⊔ ∃R.C)
A ⊓ ∀R.A ⊓ ∀R.¬∃P.A ⊓ ∃R.∃P.A
5 Wsparcie narzędziowe
Istnieje wiele implementacji silników wnioskujących dla logik deskrypcyjnych.
Niektóre z nich są zoptymalizowane pod kątem konkretnych języków DL (np. takich na których opierają się warianty języka ontologii OWL ).
Lista dostępnych silników wnioskujących dostępna jest na stronie: Prof. U. Sattler.
Popularne narzędzia to m.in:
Najczęściej silniki wnioskujące zintegrowane są z innymi narzędziami, np. edytorami ontologii (pełnią one wówczas rolę pomocniczą, np. do sprawdzania spójności ontologii itp.).
Ćwiczenie 9:
Pobierz silnik wnioskujący
Pellet.

Na borgu powinien być w
/usr/local/pellet.
Uruchom go wpisując w konsoli pellet.sh help i zapoznaj się z dostępnymi opcjami. (/usr/local/pellet/pellet.sh)
Uruchom pellet.sh consistency <ontology> gdzie <ontology> jest bazą wiedzy people+pets.owl umieszczoną w katalogu examples/data.
Jakie są rezultaty?
Uruchom pellet.sh classify <ontology> dla powyższej ontologii peopl+pets.owl
Jakie są rezultaty?
Materiały
Wykłady, prezentacje
Kursy
Narzędzia

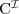 jest niepusty.
jest niepusty.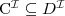 dla każdego modelu I terminologii T.
dla każdego modelu I terminologii T. dla każdego modelu I terminologii T.
dla każdego modelu I terminologii T.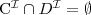 dla każdego modelu I terminologii T.
dla każdego modelu I terminologii T.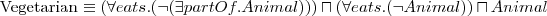
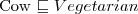
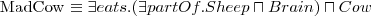
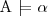 iff każda interpretacja spełniająca A spełnia również α.
iff każda interpretacja spełniająca A spełnia również α.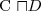 zawiera się w ⊥
zawiera się w ⊥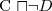 nie jest spełnialne (na tej obserwacji opierają się algorytmy tableau)
nie jest spełnialne (na tej obserwacji opierają się algorytmy tableau)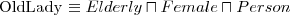
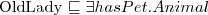

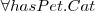
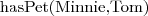 ,
,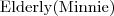 ,
,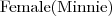
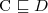 wtw. gdy wyrażenie
wtw. gdy wyrażenie 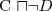 jest niespełnialne.
Schemat działania:
jest niespełnialne.
Schemat działania: