Automatyczne planowanie
Poniższe laboratorium stanowi wstęp do bardzo ważnej i wszechobecnej (przemysł, robotyka, gry komputerowe, etc.) dziedziny AI, jaką jest planowanie. Zasadniczo planowanie polega na znalezieniu ciągu akcji (zwanego planem), który po zastosowaniu na stanie początkowym S, doprowadzi do osiągnięcia stanu docelowego G. Każda akcja posiada warunki, w których może zostać wykonana oraz skutki jej zastosowania. Planowanie jest trudne, o ile nie założy się odpowiednich ograniczeń na akcje, jego złożoność jest klasy PSPACE-zupełnej (to gorzej niż problemy NP, do której zaliczają się problemy optymalizacji dyskretnej). Trzeba ponadto zauważyć, że w realnych nie zabawkowych problemach występują dodatkowe czynniki zwiększające trudność problemu:
niepełna wiedza o aktualnym stanie. Przykładem może być brak odpowiednich sensorów w robocie lub gra w karty, w której nie znamy całego rozdania, a musimy planować wiele ruchów w przód (na przykład Brydż).
niepewność wynikająca z zawodności akcji. W tym przypadku nie jesteśmy pewni, czy wykonywana akcja na pewno się uda. Prostym modelem takiej sytuacji może być gra RPG, gdzie rzut kością decyduje o sukcesie. Plan rozegrania bitwy w tego typu grze powinien brać pod uwagę możliwość nieudanego rzutu. Przykładem bardziej „życiowym” jest praca robota, który próbują podjąć pewne akcje, często akcje.
wykonywanie akcji zajmuje czas — plan powinien brać pod uwagę temporalny wymiar problemu. Wszak rzadko kiedy środowisko, w którym się poruszamy, jest statyczne i przyjazne.
mogą wydarzać się zdarzenia niezależne od agenta — np. wypadek drogowy na drodze autonomicznego samochodu. Obsługa takich wyjątków również wchodzi w zakres planowania.
Ze względu na podstawowy charakter, na tych zajęciach zajmiemy się dostatecznie trudnym problemem klasycznego planowania.
Świat klocków
 Starym i lubianym problemem klasycznego planowania jest tzw. świat klocków. Problem jest pozornie mało ambitny: polega na znalezieniu odpowiedniej sekwencji ruchów, pozwalających na przestawienie klocków ze stanu początkowego do zadanego stanu końcowego. W świecie klocków istnieje określona liczba klocków (tradycyjnie każdy klocek wyróżnia narysowana na nim literka) oraz kilka kolumn, w których te klocki mogą leżeć. Każdy klocek leży na dnie jednej z kolumn (czyli na stole) lub umieszczony jest na innym klocku. Przykładowe stany początkowy i końcowy pokazane są na obrazie powyżej. Istnieje dwie możliwe akcje w świecie klocków:
Starym i lubianym problemem klasycznego planowania jest tzw. świat klocków. Problem jest pozornie mało ambitny: polega na znalezieniu odpowiedniej sekwencji ruchów, pozwalających na przestawienie klocków ze stanu początkowego do zadanego stanu końcowego. W świecie klocków istnieje określona liczba klocków (tradycyjnie każdy klocek wyróżnia narysowana na nim literka) oraz kilka kolumn, w których te klocki mogą leżeć. Każdy klocek leży na dnie jednej z kolumn (czyli na stole) lub umieszczony jest na innym klocku. Przykładowe stany początkowy i końcowy pokazane są na obrazie powyżej. Istnieje dwie możliwe akcje w świecie klocków:
podniesienie klocka przez robota. Warunkiem wykonania tej akcji jest swobodny dostęp do klocka (nie może być przykryty innym klockiem) oraz puste ramię robota — równocześnie może być podniesiony tylko jeden klocek.
położenie klocka przez robota. Warunkiem wykonania tej akcji jest swobodny niepuste ramię robota. Klocek może być położony jedynie na szczycie kolumny.
Rozwiązywanie problemu
Istnieją trzy względnie proste metody rozwiązywania tego problemu:
A-star
Standardową reprezentacją problemów planowania jest skierowany graf nazywany przestrzenią stanów — każdy węzeł w grafie odpowiada możliwemu stanowi świata. Dwa wierzchołki są połączone krawędzią, jeśli istnieje akcja, która pozwala na przejście z jednego stanu do drugiego. Problem planowania sprowadza się wtedy do znalezienia ścieżki łączącej wybrany wierzchołek (stan początkowy) z innym wierzchołkiem (stanem końcowym). Problem jest często ogromny (potencjalnie nieskończony) rozmiar przestrzeni stanów i brak oczywistych metod jej przeszukiwania. Poniżej pokazany jest przykład przestrzeni stanów dla bardzo prostej instancji problemu świata klocków:
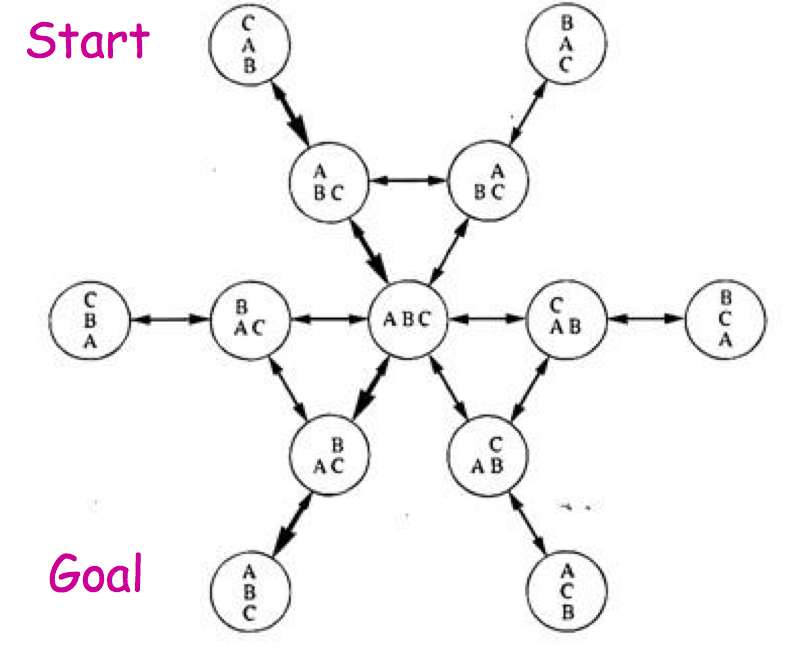
Podstawową metodą przeszukiwania przestrzeni stanów jest zastosowanie heurystycznych algorytmów, np. A-star. Problemem tego podejścia jest zależność od heurystyki, która musi być dopuszczalna i nie przenosi się łatwo do innych problemów tego typu. Z drugiej strony jednak to właśnie dobrze dobrana heurystyka często sprawia, że problem daje rozwiązać się w rozsądnym czasie (dlatego też aktualnie jest wkładane dużo wysiłku w automatyczne odkrywanie heurystyk).
Zadania
proszę zdefiniować dopuszczalną heurystykę dla problemu świata klocków
Kodowanie do problemu satysfakcji ograniczeń
Często stosowanym podejściem w problemach posiadających rozbudowaną strukturę jest przetłumaczenie problemu planowania do problemu satysfakcji ograniczeń i zastosowanie istniejącego solvera. Takie tłumaczenie wiąże się jednak z pewnymi trudnościami:
w problemach satysfakcji ograniczeń istnieje jeden globalny stan (aktualne wartości zmiennych). Aby modelować systemy stanowe, należy najczęściej zdefiniować po jednej kopii wszystkich zmiennych stanowych dla każdej chwili czasowej problemu. Następnie ograniczeniami wymusza się, aby następujące po sobie stany spełniały odpowiednie warunki.
problem planowania może nie zakładać żadnego horyzontu czasowego („deadline'u”), podczas, gdy w problemach dyskretnych nie mogą istnieć zmienne o nieskończonej dziedzinie. W horyzont czasowy reprezentuje się wtedy jako skończoną (dostatecznie dużą) wartość. Aby konstruować jak najkrótsze plany często wymusza się na solverze, by najpierw próbował przypisywać horyzontowi czasowemu jak najmniejsze wartości.
Zadania
-
świat bloków opisany w tym modelu jest uproszczoną wersją problemu opisanego powyżej. Na czym polegają wprowadzone uproszczenia?
które ograniczenia definiuje sposób przechodzenia między stanami?
proszę teraz:
zwiększyć wartość maksymalnej liczby kroków do odpowiednio dużej wartości - jaki ma to wpływ na długość planu?
zmienić definicję ostatniego kroku (parametr end) tak, aby był on zmienną o odpowiedniej dziedzinie
zmienić definicję ograniczenia definiującego przejścia między stanami tak, aby przejście te następowały jedynie, gdy indeks czasowy stanu nie przekracza wartości nowej zmiennej end
zmienić adnotację przy definicji celu tak, aby solver starał się zaczynać zawsze od jak najmniejszej wartości zmiennej end
proszę poprawić wypisywanie wyniku tak, aby wypisywało tylko istotne stany
Program planujący
Innym rozwiązaniem jest zastosowania generycznego programu planującego, który przyjmując na wejściu definicję problemu, będzie w stanie znaleźć dopuszczalny plan. Jednym z najbardziej znanych programów planujących jest powstały na Stanfordzie w latach 70 program STRIPS. Używana w nim reprezentacja wiedzy jest do dzisiaj podstawą większości narzędzi planujących. Przykładowa struktura problemu może być zdefiniowana następująco:
Mając taką reprezentację wiedzy, klasyczny program planujący działa według bardzo prostego wzorca (dla zadanego stanu końcowego G i początkowego S):
Sprawdź, czy aktualny stan jest stanem końcowym. Jeżeli tak, wypisz znaleziony plan.
Znajdź fakt F, który jest prawdziwy w stanie końcowym, ale nie jest prawdziwy aktualnym stanie.
Znajdź akcję A, która posiada w liście faktów dodawanych fakt F.
Uruchom rekurencyjnie rutynę planującą, aby znaleźć plan doprowadzający do stanu, który spełnia warunki wykonania akcji A.
Wykonaj akcję A i zaktualizuj aktualny stan do stanu S'.
Uruchom rutynę planującą zaczynając od nowego stanu S'.
Efektem powyższej procedury będzie „odwrócony plan”, aby miał sens, należy go wypisać idąc od końca. Drugi haczyk polega na unikaniu zapętlenia w planowaniu - jeżeli chcemy osiągnąć warunki wykonania akcji A (punt 4.) należy wyłączyć ją z procesu planowania.
Zadania
Należy pobrać
kod programu planującego i otworzyć go w edytorze tekstu lub
wygodnym środowisku on-line. W miarę możliwości (i znajomości prologa) proszę zapoznać się z implementacją plannera STRIPS na końcu pliku. Następnie należy uzupełnić go o informacje potrzebne do rozwiązania problemu bloków (sekcje
%TODO:). Objaśnienia:
dla wygody planowania możemy pominąć numery kolumn, a stan może być reprezentowane przez pięć typów faktów (przykładowe stany można zobaczyć w sekcji EXAMPLES OF USAGE):
ontable/1 — dany klocek leży na stole, np. ontable(a)
on/2 — dany klocek leży na drugim klocku, np. on(a,b)
clear/1 — na danym klocku nic nie leży, np. clear(a)
holding/1 — dany klocek został właśnie podniesiony, np. holding(a)
handempty/0 — żaden klocek nie jest aktualnie podniesiony, czyli: handempty
potrzebne są cztery rodzaje akcji (jedna z nich już jest zaimplementowana)
połóż klocek X na klocku Y: wykonalna, o ile klocek X jest aktualnie trzymany, a Y jest czysty. Po wykonaniu akcji klocek X leży na klocku Y i jest czysty, klocek Y przestaje być czysty i żaden klocek nie jest aktualnie podniesiony.
zdejmij klocek X z klocka Y: wykonalna, o ile klocek X jest czysty i aktualnie leży na klocku Y. Po wykonaniu akcji klocek X przestaje być czysty, przestaje leżeć na klocku Y i zostaje podniesiony. Klocek Y natomiast staje się czysty.
połóż klocek X na stole: analogicznie do akcji pierwszej z taką różnicą, że nie ma wymagań i zmian względem Y
zdejmij klocek X ze stołu: analogicznie do akcji drugiej
Proszę uruchomić planowanie dla trzech załączonych przykładów oraz dla jednej zamodelowanego samodzielnie.
Proszę usunąć z części warunkowej akcji wszystkie warunki o postaci clear/1 i ponownie uruchomić planowanie dla czterech przypadków.
jaką wartość mają tak wygenerowane plany?
-

