This is an old revision of the document!
The XTT^2 ALSV(FD) Specification
Author: Grzegorz J. Nalepa, based on the work with Antoni Ligêza
Version: Draft 2008Q3
Introduction to Attributive Logics
Attributive logics constitute a simple yet widely-used tool for knowledge specification and development of rule-based systems.
In fact in a large variety of applications in various areas of Artificial Intelligence (AI) and Knowledge Engineering (KE) attributive languages constitute the core knowledge representation formalism.
The most typical areas of applications include rule-based systems, expert systems (ones based on rule formalism) and advanced database and data warehouse systems with knowledge discovery applications and contemporary business rules and business intelligence components.
The description of AL presented here is based on several papers, including
ALSV(FD)
In SAL (Set Attributive Logic) as well as in its current version ALSV(FD), the very basic idea is that attributes can take atomic or set values.
After (ali2005thebook) it is assumed that an attribute A_i is a function (or partial function) of the form
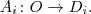 Here O is a set of objects and D_i is the domain of attribute A_i.
Here O is a set of objects and D_i is the domain of attribute A_i.
A generalized attribute A_i is a function (or partial function) of the form
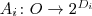 where 2^D_i is the family of all the subsets of D_i.
where 2^D_i is the family of all the subsets of D_i.
The basic element of the language of Attribute Logic with Set Values over Finite Domains (ALSV(FD) for short) are attribute names and attribute values.
For simplicity of presentation no objects are considered here; in practice, the same attribute applied to two (or more) different objects can be considered as two (or more) new, different, object-labelled attributes. Moreover, unless two (or more) different objects are considered at the same time, no explicite reference to an object is necessary.
Let us consider:
Let
A = A_1, A_2, … ,A_n
be all the attributes such that their values define the state of the system under consideration.
It is assumed that the overall domain D is divided into n sets (disjoint or not),
D} = D_1 u D_2 u … u D_n,
where D_i is the domain related to attribute
A_i, i=1,2, … ,n.
Any domain D_i is assumed to be a finite (discrete) set.
The set can be ordered, partially ordered, or unordered; in case of ordered (partially ordered) sets some modifications of the notation are allowed.
As we consider dynamic systems, the values of attributes can change over time (or state of the system).
We consider both simple attributes of the form
A_i : T → D_{i}
(i.e. taking a single value at any instant of time) and
generalized ones of the form
A_i: T → 2^D_i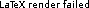 A_{i} = d
A_{i} = d A_{i} \neq d
A_{i} \neq d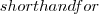 A_{i} \in D_{i}\setminus \{d \}.
A_{i} \in D_{i}\setminus \{d \}. A_{i} \in V_{i}
A_{i} \in V_{i}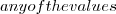 d\in V_{i}
d\in V_{i} (A_{i} = d_{1})\otimes (A_{i} = d_{2})\otimes\ldots \otimes (A_{i} = d_{k})
(A_{i} = d_{1})\otimes (A_{i} = d_{2})\otimes\ldots \otimes (A_{i} = d_{k}) V_{i} = \{d_{1}, d_{2},\ldots,d_{k} \}
V_{i} = \{d_{1}, d_{2},\ldots,d_{k} \}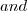 \otimes
\otimes A_{i} \not\in V_{i}
A_{i} \not\in V_{i} A_{i} \in D_{i}\setminus V_{i}
A_{i} \in D_{i}\setminus V_{i} A_{i} = V_{i}
A_{i} = V_{i} V_{i}
V_{i} A_{i} \neq V_{i}
A_{i} \neq V_{i}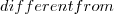 V_{i}
V_{i} A_{i} \subseteq V_{i}
A_{i} \subseteq V_{i}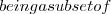 V_{i}
V_{i} A_{i} \supseteq V_{i}
A_{i} \supseteq V_{i}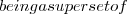 V_{i}
V_{i} A \sim V_{i}
A \sim V_{i}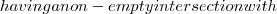 V_{i}
V_{i}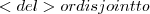 V_{i}
V_{i} A_{i} \not\sim V_{i}
A_{i} \not\sim V_{i}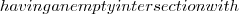 V_{i}
V_{i}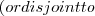 V_{i}
V_{i}![Math $) &
\texttt{notsim} & \\ \hline
\end{tabular}
\end{table}
</latex>
Table 2: Generalized attribute formulas syntax
In case V_i is an empty set (the attribute takes in fact no value) we shall write A_i = ' '.
See [[hekate:alsvdf#any and null]]
More complex formulae can be constructed with //conjunction// ''^'' ($](/lib/exe/fetch.php?media=wiki:latex:/img443f1c9520feac9f732f19f391f0451e.png) \wedge
\wedge A = V
A = V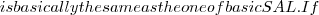 V = \{d_{1}, d_{2},\ldots, d_{k} \}
V = \{d_{1}, d_{2},\ldots, d_{k} \}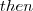 A = V
A = V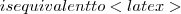 A \supseteq \{d_{1}\}\wedge A \supseteq \{d_{2}\}\wedge\ldots\wedge A \supseteq \{d_{k}\}
A \supseteq \{d_{1}\}\wedge A \supseteq \{d_{2}\}\wedge\ldots\wedge A \supseteq \{d_{k}\}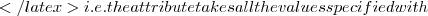 V
V A\subseteq V
A\subseteq V A \supseteq V
A \supseteq V A \sim V
A \sim V A\subseteq V \equiv A=U
A\subseteq V \equiv A=U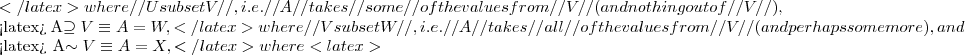 V \cap X \neq \emptyset
V \cap X \neq \emptyset \frac{A \supseteq W}{A \supseteq V}
\frac{A \supseteq W}{A \supseteq V}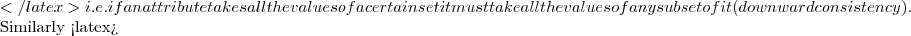 \frac{A \subseteq V}{A \subseteq W}
\frac{A \subseteq V}{A \subseteq W} \models
\models A=d_{j}
A=d_{j} A\neq d_{j}
A\neq d_{j} A \in V_{j}
A \in V_{j} A \not\in V_{j}
A \not\in V_{j} A=d_{i}
A=d_{i} d_{i} = d_{j}
d_{i} = d_{j} d_{i}\neq d_{j}
d_{i}\neq d_{j} d_{i}\in V_{j}
d_{i}\in V_{j} d_{i}\not\in V_{j}
d_{i}\not\in V_{j} A \neq d_{i}
A \neq d_{i} d_{i} = d_{j}
d_{i} = d_{j} V_{j} = D\setminus \{d_{i}\}
V_{j} = D\setminus \{d_{i}\} V_{j} = \{d_{i} \}
V_{j} = \{d_{i} \} A \in V_{i}
A \in V_{i} V_{i} = \{d_{j} \}
V_{i} = \{d_{j} \} d_{j}\not\in V_{i}
d_{j}\not\in V_{i} V_{i}\subseteq V_{j}
V_{i}\subseteq V_{j} V_{i}\cap V_{j} = \emptyset
V_{i}\cap V_{j} = \emptyset A \not\in V_{i}
A \not\in V_{i} D\setminus V_{i} = \{d_{j}\}
D\setminus V_{i} = \{d_{j}\} V_{i} = \{d_{j}\}
V_{i} = \{d_{j}\} V_{j}=D\setminus V_{i}
V_{j}=D\setminus V_{i} V_{j}\subseteq V_{i}
V_{j}\subseteq V_{i} \models
\models A=W
A=W A\neq W
A\neq W A\subseteq W
A\subseteq W A \supseteq W
A \supseteq W A \sim W
A \sim W A \not\sim W
A \not\sim W A=V
A=V V=W
V=W V\neq W
V\neq W V\subseteq W
V\subseteq W V\supseteq W
V\supseteq W V\cap W\neq \emptyset
V\cap W\neq \emptyset V\cap W = \emptyset
V\cap W = \emptyset A\neq V
A\neq V V=W
V=W W = D
W = D W = D
W = D A \subseteq V
A \subseteq V V \subset W
V \subset W V\subseteq W
V\subseteq W W = D
W = D V\cap W = \emptyset
V\cap W = \emptyset A \supseteq V
A \supseteq V W \subset V
W \subset V W = D
W = D V\supseteq W
V\supseteq W V\cap W \neq \emptyset
V\cap W \neq \emptyset A \sim V
A \sim V V\cap W=\emptyset
V\cap W=\emptyset W = D
W = D V=W
V=W A\not\sim V
A\not\sim V V\cap W\neq\emptyset
V\cap W\neq\emptyset W = D
W = D W=D
W=D V=W
V=W A\subseteq V\wedge A\subseteq W
A\subseteq V\wedge A\subseteq W V\cap W=\emptyset
V\cap W=\emptyset \not\models
\not\models A=W
A=W A\subseteq W
A\subseteq W A \supseteq W
A \supseteq W A \sim W
A \sim W A=V
A=V W\neq V
W\neq V V \not\subseteq W
V \not\subseteq W W\not\subseteq V
W\not\subseteq V V\cap W \neq \emptyset
V\cap W \neq \emptyset A \subseteq V
A \subseteq V W\not\subseteq V
W\not\subseteq V V\cap W = \emptyset
V\cap W = \emptyset W\not\subseteq V
W\not\subseteq V W\cap V =\emptyset
W\cap V =\emptyset A \supseteq V
A \supseteq V V\not\subseteq W
V\not\subseteq W V\not\subseteq W
V\not\subseteq W A \sim V
A \sim V V\cap W \neq \emptyset
V\cap W \neq \emptyset W\not\subseteq V
W\not\subseteq V (A_{1}\propto_{1} V_{1})\wedge (A_{2}\propto_{2} V_{2})\wedge \ldots (A_{n}\propto_{n} V_{n}) \longrightarrow \mathit{RHS}
(A_{1}\propto_{1} V_{1})\wedge (A_{2}\propto_{2} V_{2})\wedge \ldots (A_{n}\propto_{n} V_{n}) \longrightarrow \mathit{RHS} (A_{1}=S_{1})\wedge(A_{2}=S_{2})\wedge \ldots \wedge (A_{n}=S_{n})
(A_{1}=S_{1})\wedge(A_{2}=S_{2})\wedge \ldots \wedge (A_{n}=S_{n})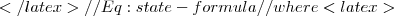 S_{i} = d_{i}
S_{i} = d_{i} d_{i}\in D_{i}
d_{i}\in D_{i}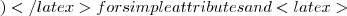 S_{i}= V_{i}
S_{i}= V_{i}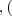 V_{i}\subseteq D_{i}$)
</latex>
for complex.
V_{i}\subseteq D_{i}$)
</latex>
for complex.
Any and NULL
 ALi
In case the value of A_i is unspecified we shall write A_i = NULL (a database convention).
ALi
In case the value of A_i is unspecified we shall write A_i = NULL (a database convention).
Following a Prolog convention and logic, a ANY attribute value is possible in comparison (see_ in Prolog).
The semantics can be: “any value”, “not important”, etc.
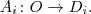 Here O is a set of objects and D_i is the domain of attribute A_i.
Here O is a set of objects and D_i is the domain of attribute A_i.
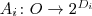 where 2^D_i is the family of all the subsets of D_i.
where 2^D_i is the family of all the subsets of D_i.
 A_{i} = d
A_{i} = d A_{i} \in D_{i}\setminus \{d \}.
A_{i} \in D_{i}\setminus \{d \}. A_{i} \in V_{i}
A_{i} \in V_{i} d\in V_{i}
d\in V_{i}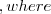 V_{i} = \{d_{1}, d_{2},\ldots,d_{k} \}
V_{i} = \{d_{1}, d_{2},\ldots,d_{k} \}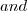 \otimes
\otimes A_{i} \not\in V_{i}
A_{i} \not\in V_{i}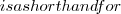 A_{i} \in D_{i}\setminus V_{i}
A_{i} \in D_{i}\setminus V_{i}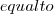 V_{i}
V_{i} A_{i} \neq V_{i}
A_{i} \neq V_{i}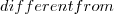 V_{i}
V_{i} A_{i} \subseteq V_{i}
A_{i} \subseteq V_{i}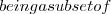 V_{i}
V_{i} A_{i} \supseteq V_{i}
A_{i} \supseteq V_{i}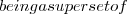 V_{i}
V_{i} A \sim V_{i}
A \sim V_{i}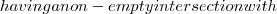 V_{i}
V_{i}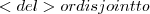 V_{i}
V_{i} A_{i} \not\sim V_{i}
A_{i} \not\sim V_{i}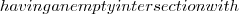 V_{i}
V_{i}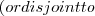 V_{i}
V_{i}![Math $) &
\texttt{notsim} & \\ \hline
\end{tabular}
\end{table}
</latex>
Table 2: Generalized attribute formulas syntax
In case V_i is an empty set (the attribute takes in fact no value) we shall write A_i = ' '.
See [[hekate:alsvdf#any and null]]
More complex formulae can be constructed with //conjunction// ''^'' ($](/lib/exe/fetch.php?media=wiki:latex:/img443f1c9520feac9f732f19f391f0451e.png) \wedge
\wedge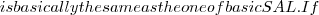 V = \{d_{1}, d_{2},\ldots, d_{k} \}
V = \{d_{1}, d_{2},\ldots, d_{k} \}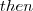 A = V
A = V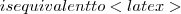 A \supseteq \{d_{1}\}\wedge A \supseteq \{d_{2}\}\wedge\ldots\wedge A \supseteq \{d_{k}\}
A \supseteq \{d_{1}\}\wedge A \supseteq \{d_{2}\}\wedge\ldots\wedge A \supseteq \{d_{k}\} V
V A\subseteq V
A\subseteq V A \supseteq V
A \supseteq V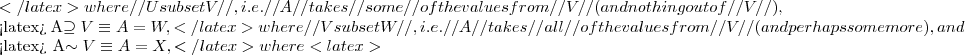 V \cap X \neq \emptyset
V \cap X \neq \emptyset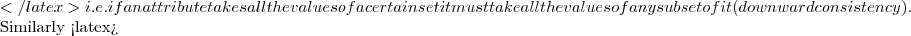 \frac{A \subseteq V}{A \subseteq W}
\frac{A \subseteq V}{A \subseteq W} A=d_{j}
A=d_{j} A\neq d_{j}
A\neq d_{j} A \in V_{j}
A \in V_{j} A \not\in V_{j}
A \not\in V_{j} A=d_{i}
A=d_{i} d_{i}\neq d_{j}
d_{i}\neq d_{j} d_{i}\in V_{j}
d_{i}\in V_{j} A \neq d_{i}
A \neq d_{i} d_{i} = d_{j}
d_{i} = d_{j} V_{j} = \{d_{i} \}
V_{j} = \{d_{i} \} A \in V_{i}
A \in V_{i} V_{i} = \{d_{j} \}
V_{i} = \{d_{j} \} V_{i}\subseteq V_{j}
V_{i}\subseteq V_{j} A \not\in V_{i}
A \not\in V_{i} A=W
A=W A=V
A=V V=W
V=W A\neq V
A\neq V V=W
V=W W = D
W = D W = D
W = D A \subseteq V
A \subseteq V V \subset W
V \subset W W = D
W = D V\cap W = \emptyset
V\cap W = \emptyset A \supseteq V
A \supseteq V W \subset V
W \subset V W = D
W = D V\supseteq W
V\supseteq W A \sim V
A \sim V V\cap W=\emptyset
V\cap W=\emptyset V=W
V=W A\not\sim V
A\not\sim V V\cap W\neq\emptyset
V\cap W\neq\emptyset W=D
W=D V\cap W=\emptyset
V\cap W=\emptyset A\subseteq W
A\subseteq W A=V
A=V A \subseteq V
A \subseteq V W\cap V =\emptyset
W\cap V =\emptyset A \sim V
A \sim V V\cap W \neq \emptyset
V\cap W \neq \emptyset W\not\subseteq V
W\not\subseteq V (A_{1}\propto_{1} V_{1})\wedge (A_{2}\propto_{2} V_{2})\wedge \ldots (A_{n}\propto_{n} V_{n}) \longrightarrow \mathit{RHS}
(A_{1}\propto_{1} V_{1})\wedge (A_{2}\propto_{2} V_{2})\wedge \ldots (A_{n}\propto_{n} V_{n}) \longrightarrow \mathit{RHS} S_{i} = d_{i}
S_{i} = d_{i} d_{i}\in D_{i}
d_{i}\in D_{i}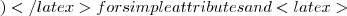 S_{i}= V_{i}
S_{i}= V_{i}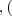 V_{i}\subseteq D_{i}$)
</latex>
for complex.
V_{i}\subseteq D_{i}$)
</latex>
for complex.
 ALi
In case the value of A_i is unspecified we shall write A_i = NULL (a database convention).
ALi
In case the value of A_i is unspecified we shall write A_i = NULL (a database convention).