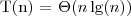Obliczanie złożoności algorytmów
Do przygotowania
Znajomość i rozumienie pojęć:
Złożoność obliczeniowa.
Złożoność pamięciowa.
Złożoność pesymistyczna.
Złożoność oczekiwana.
Złożoność optymistyczna.
Przykłady
Metoda podstawiania
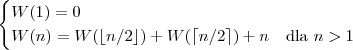
Jak sobie radzimy z rekurencją? Podstawiamy 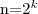 .
Wtedy mamy:
.
Wtedy mamy:
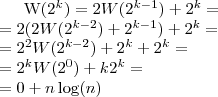
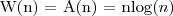
Kolejny przykład metody podstawiania:
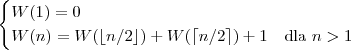
oraz
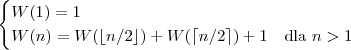
W obu powyższych przykładach robimy to samo podstawienie i możemy zaobserwować że złożoność jest liniowa. Wyprowadzenie:
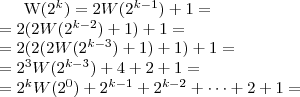
Teraz dla przypadku kiedy
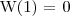
:
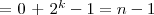
oraz dla przypadku kiedy
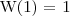
:
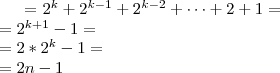
Jeszcze jeden przykład:
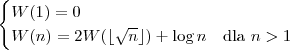
Rozwiązanie powyższego przykładu jest następujące:
Wstawiamy
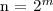
, czyli
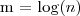
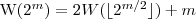
następnie wykonujemy kolejne podstawienie:
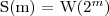
i w ten sposób otrzymujemy:
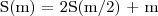
co jest równe:
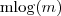
Powracając i wstawiając do wcześniejszego wzoru otrzymujemy:
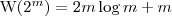
i ostatecznie wstawiając
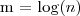
dostajemy:
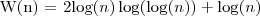
co daje złożoność:
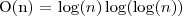
Metoda rekurencji uniwersalnej
Umożliwia szybkie wyznaczanie rozwiązania równania rekurencyjnego postaci:
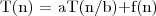
gdzie:
Teraz może prosty przykład:
Mamy równanie:
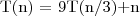
Rozwiązanie:
Drugi przykład:
Mamy równanie:
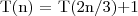
Rozwiązanie:
Trzeci przykład:
Mamy równanie:
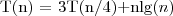
Rozwiązanie:
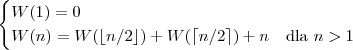
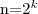 .
Wtedy mamy:
.
Wtedy mamy: 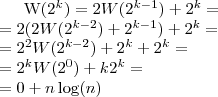
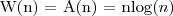
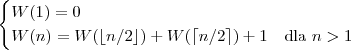
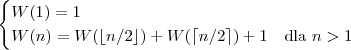
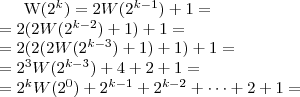
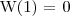 :
: 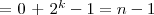
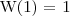 :
: 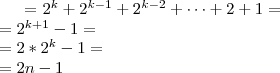
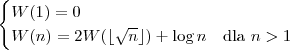
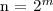 , czyli
, czyli 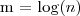
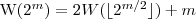
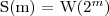
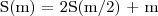
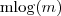
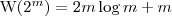
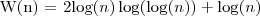
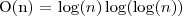
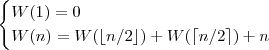
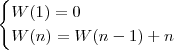
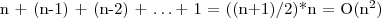
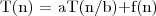
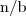 interpretujemy jako
interpretujemy jako 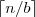 lub jako
lub jako 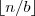
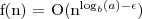 dla pewnej stałej ε > 0 to,
dla pewnej stałej ε > 0 to, 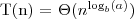
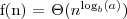 to,
to, 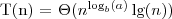
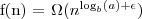 dla pewnej stałej ε > 0 oraz
dla pewnej stałej ε > 0 oraz 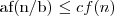 dla pewnej stałej c i wszystkich dostatecznie dużych n, to
dla pewnej stałej c i wszystkich dostatecznie dużych n, to 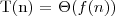
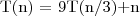
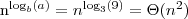
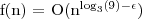 , gdzie ε = 1 to możemy zastosować przypadek 1 z twierdzenia i wywnioskować że
, gdzie ε = 1 to możemy zastosować przypadek 1 z twierdzenia i wywnioskować że 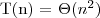
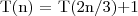
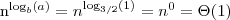
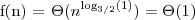 , i z twierdzenia możemy wywnioskować że
, i z twierdzenia możemy wywnioskować że 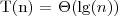
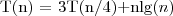
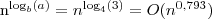
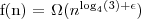 , gdzie ε ≈ 0,2 więc stosuje się przypadek 3 jeżeli tylko możemy pokazać, że f(n) spełnia warunek regularności:
, gdzie ε ≈ 0,2 więc stosuje się przypadek 3 jeżeli tylko możemy pokazać, że f(n) spełnia warunek regularności: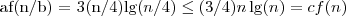 dla n=3/4.
dla n=3/4.