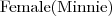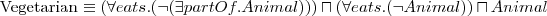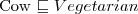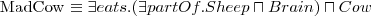To jest stara wersja strony!
KRR: Logiki Deskrypcyjne
Tematem laboratorium są logiki deskrypcyjne (ang. Description Logics).
W zakres ćwiczeń wchodzą następujące tematy:
DL jako formalizm reprezentacji wiedzy
Struktura bazy wiedzy w DL
Zadania wnioskowania dla DL
Wsparcie narzędziowe
1 Reprezentacja wiedzy z użyciem Logik Deskrypcyjnych
1.1 Wprowadzenie
Logiki deskrypcyjne (opisowe) (ang. Description Logics, DL) są rodziną formalizmów reprezentacji wiedzy.
Elementami reprezentacji są
pojęcia (klasy),
role (relacje) i
instancje (obiekty
1)).
Logiki opisowe są koncepcyjnie powiązane z sieciami semantycznymi (ang. semantic networks) i ramami (ang. frames), jednak w przeciwieństwie do nich, przez swoje powiązanie z logiką pierwszego rzędu, posiadaję formalnie zdefiniowaną semantykę i zapewniają możliwość automatycznego wnioskowania.
Przykład 1: graf obrazujący zbiór obiektów powiązanych relacjami i należących do pewnych klas:
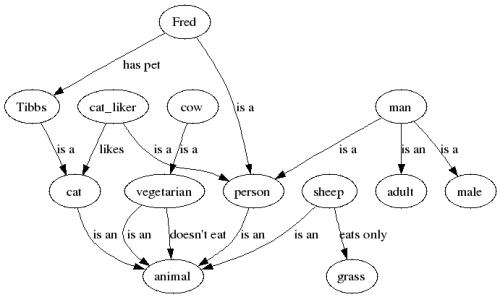
Wybrane fragmenty ww. grafu zapisane w logice opisowej:
1.2 Co możemy zapisać z użyciem Logik Deskrypcyjnych
W logikach opisowych możemy konstruować zdania o pojęciach i instancjach.
Poniżej przedstawiono podstawowe rodzaje wyrażeń w logice opisowej i ich intuicyjne wytłumaczenia:
Instancje (obiekty):
przynależność obiektu do klasy (ang. concept assertions), np:
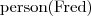
- Fred jest osobą
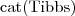
Tibbs jest kotem
relacja między dwoma obiektami
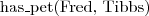
- Fred ma zwierzę, którym jest Tibbs
Pojęcia
definicje pojęć (warunki konieczne i wystarczające), np.
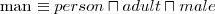
- Mężczyzna to dorosła osoba rodzaju męskiego
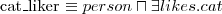
- Miłośnik kotów to osoba taka, że istnieje kot, którego ta osoba lubi
relacje między pojęciami (klasami)
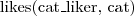
- (każdy) miłośnik kotów lubi (jakiegoś) kota
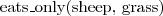
- (każda) owca je tylko trawę
aksjomaty
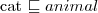
kot jest zwierzęciem (hierarchia pojęć)
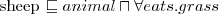
owce to zwierzęta, które jedzą tylko trawę (warunek konieczny, ale nie wystarczający)
Ćwiczenie 1:
Wypisz z grafu z przykładu 1 wszystkie:
pojęcia (klasy),
role (relacje),
instancje (obiekty).
Odpowiedzi: lab_dl_answers
1.3 Podstawowy język DL
W języku logiki opisowej tworzymy opisy.
Podstawowe elementy języka to: atomicze pojęcia i atomiczne role.
Złożone opisy tworzy się indukcyjnie za pomocą konstruktorów.
Poszczególne logiki opisowe różnią się między sobą zbiorem dopuszczalnych konstruktorów
Najprostszy język: AL
Składnia AL
atomiczne pojęcia (
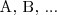
)
atomiczne role (
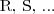
)
opisy (
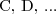
); mogą nimi być:
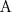
- pojęcie atomiczne

-
top concept, pojęcie uniwersalne oznaczające „wszystko”
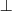
-
bottom concept, pojęcie puste, oznaczające „nic”
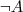
- negacja
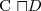
- koniunkcja
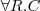
- kwantyfikator uniwersalny: „dla każdego”
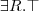
- kwantyfikator egzystencjalny/szczegółowy: „istnieje”
Semantyka AL
1.4 Rodzina języków DL
Poszczególne języki DL rozróżniamy poprzez konstruktory, które dopuszczają.
Przykładowe konkstruktory:
Używające powyższych konstruktorów języki nazywają się odpowiednio:
-
-
-
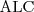
→ odpowiada podzbiorowi logiki pierwszego rzędu ograniczonemu do formuł z dwoma zmiennymi
1.5 Powiązanie z innymi rachunkami (logicznymi)
* Rozszerzenia języków DL
Podstawowym językiem jest ALC (≈ALUE).
Dodatkowe litery oznaczają następujące rozszerzenia:
dotyczące konstruktorów pojęć:
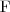
ograniczenia funkcyjne (np. ≤1
hasMother)
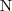
ograniczenia liczbowe (np. ≥2
hasChild, ≤
3hasChild)
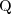
warunkowe ograniczenia liczbowe (np. ≥2
hasChild.Doctor))
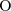
z użyciem instancji (e.g., {Italy})
dotyczące konstruktorów ról:
dodatkowe aksjomaty dot. ról:
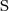
przechodniość relacji

hierarchia relacji (e.g.,
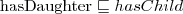
)
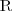
zawieranie się relacji: RoS ⊆ R, RoS ⊆
inne:
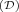
użycie typów danych w obrębie języka
Przykłady:
Język ontologii
OWL DL jest równoważny
SHOIN(D) przechodniość (S) + hierarhia ról (H) + instancje (O) + odwrotność (I) + ograniczenia liczbowe (N) + typy danych (D) = SHOIN(D)
OWL Lite jest uproszczonym podzbiorem OWL DL i odpowiada
SHIF(D) przechodniość (S) + hierarchia (H) + odwrotność (I) + funkcyjność (F) + typy danych (D)= SHIF(D)
OWL2 - ekspresywny język ontologii równoważny
SROIQ(D) R - zawieranie się relacji (RoS ⊆ R, RoS ⊆ S)
BONUS:
Złożoność obliczeniowa wnioskowania w poszczególnych językach DL zależy od ich siły ekspresji: zobacz
przewodnik po językach DL
Reprezentacja wiedzy: Zadania
Rozważmy interpretację: I = (∆, ·I ), gdzie
Przedstaw powyższą interpretację w postaci grafu.
Zapisz następujące opisy w logice deskrypcyjnej:
Ci którzy są w związku małżeńskim z doktorem i posiadający psa jako zwierzę domowe.
Ci którzy nie są w związku małżeńskim, a wszyscy ich przyjaciele są albo kobietami albo mężczyznami w związkach małżeńskich.
Wyznacz rozszerzenie powyższych pojęć w interpretacji I (sprawdź czy/kto w podanej interpretacji zalicza się do tych grup).
Zapisz następujące pojęcia w postaci aksjomatów (postaci
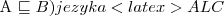
:
Ci, którzy nie mają męskich przyjaciół, nie mają zwierząt domoych.
Wszyscy mężczyźni są albo w związku małżeńskim albo mają nie-męskiego przyjaciela.
Czy te aksjomaty są prawdziwe w danej interpretacji?
Odpowiedzi: reprezentacja_-_zadania
2 Struktura bazy wiedzy opartej na logice opisowej
Baza wiedzy w logice opisowej składa się z:
Terminologii, tzw. TBox (ang. terminology box), zawierającej aksjomaty dot. pojęć, w tym definicje
Zbioru twierdzeń , tzw. ABox (ang. assertion box) - zawierającego twierdzenia o pojedynczych obiektach
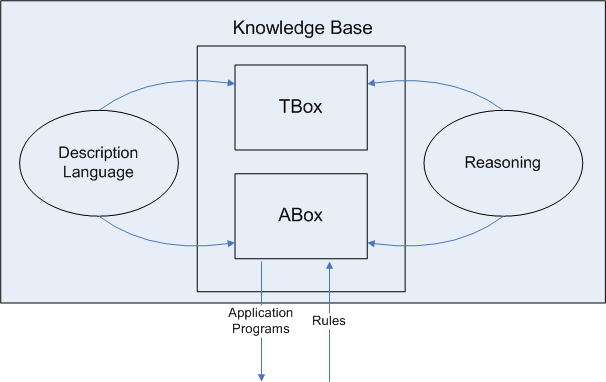
2.1 Terminologia (TBox)
Składnia:
TBox to skończony zbiór aksjomatów terminologicznych postaci:
-
lub
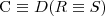
Definicje to równości, które po leweje stronie mają pojęcie atomiczne
Semantyka:
Ćwiczenie 3:
Zapisz poniższe TBox'y w postaci zdań oraz zobrazuj je za pomocą grafów:
| Lp. | Aksjomaty |
| TBox 1 | 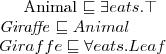 |
| TBox 2 | 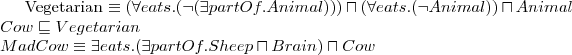 |
| TBox 3 | 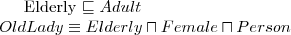 |
| TBox 4 | 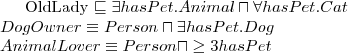 |
2.2 Opis świata (ABox)
Składnia: ABox zawiera wiedzę o instancjac (obiektach występujących w opisywanym świecie), w tym:
Semantyka:
Ćwiczenie 4
Dany jest następujący opis świata (ABox):


3 Wnioskowanie w logikach deskrypcyjnych
Logiki opisowe, dzięki formalnemu ugruntowaniu w logice, umożliwiają automatyczne wnioskowanie.
Osobne zadania wnioskowania definiuje się dla TBoxa i ABoxa.
-
Podstawowymi algorytmami dla DL są:
Złożoność obliczeniona poszczególnyc zadań wnioskowania zależy od siły ekspresji języka DL

3.1 Zadania wnioskowania dla TBoxa
Spełnialność (ang. satisfiability)
Pojęcie C jest
spełnialne względem terminologii T jeżeli istnieje model (interpretacja) I taki że
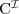
jest niepusty.
Subsumcja
2) (ang.
subsumption)
Pojęcie C jest włączone w pojęcie D wzg. T jeżeli
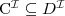
dla każdego modelu I terminologii T.
Równoważność (ang. equivalence)
Dwa pojęcia C i D są sobie
równoważne wzg. T jeżeli

dla każdego modelu I terminologii T.
Rozłączność (ang. disjointness)
Dwa pojęcia C i D są
rozłączne wzg. T. jeżeli
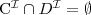
dla każdego modelu I terminologii T.
3.2 Zadania wnioskowania dla ABoxa
Sprawdzenie spójności (ang. consistency checking)
Sprawdzanie instancji (ang. instance checking)
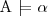
iff każda interpretacja spełniająca A spełnia również α.
Poszukiwanie najbardziej szegółowego pojęcia dla danej instancji (ang. realization).
Poszukiwanie instancji danego pojęcia (ang. retrieval).
Uwaga:
3.3 Założenie o otwartości świata
Analogia bazy wiedzy DL i relacyjnej bazy danych:
W przeciwieństwie do relacyjnych baz danych, brak w ABox oznacza brak wiedzy, nie zaś negatywnąinformację
ABox reprezentuje potencjalnie nieskończenie wiele interpretacji.
Semantyka otwartego świata wymaga nietrywialnych mechanizmów wnioskowania, a realizaja zapytań jest bardziej skomplikowana.
3.4 Algorytmy wnioskowania
Strukturalne
Porównują strukturę składniową pojęć.
Są efektywne, ale odpowiednie tylko do prostych języków, np. nie działają dla języków z negacją i dysjunkcją
Tableau
Opierają swoje działanie na obserwacji, że: 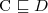 wtw. gdy wyrażenie
wtw. gdy wyrażenie 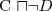 jest niespełnialne.
Schemat działania:
jest niespełnialne.
Schemat działania:
Start od faktów (aksjomatów ABox)
Dekompozycja składniowa z użyciem odpowiednich reguł tzw. tableaux expansion rules
reguły odpowiadają poszczególnymkonstruktorom (
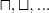
)
niektóre reguły są niedeterministyczne (np.
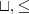
) (w praktyce prowadzi to do przeszukiwania)
Wnioskowanie o ograniczeniach na elementach modelu
Stop, kiedy nie można zastosować więcej reguł lub wystąpiła sprzeczność
Ćwiczenie
Wiedząc, że:
Czy każda starsza pani musi mieć kota? Dlaczego?
Do jakiej klasy należy obiekt Minnie?
Do jakiej klasy należy obiekt Tom?
Wiedząc, że:
-
-
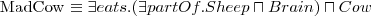
Odpowiedz na pytanie:
Jakiemu pojęciu jest równoważne pojęcie MadCow?
Odpowiedzi: wnioskowanie
BONUS:
3.5 Wsparcie narzędziowe
Silniki wnioskujące dla DL
Zadania
4 Dla zainteresowanych
Literatura, materiały
-
Portal o logikach opisowych:
Wikipedia:

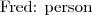 ,
,  ,
, 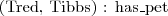
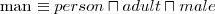 ,
, 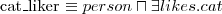
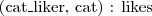 ,
, 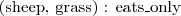
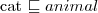 ,
, 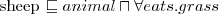
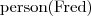 - Fred jest osobą
- Fred jest osobą 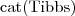 Tibbs jest kotem
Tibbs jest kotem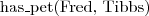 - Fred ma zwierzę, którym jest Tibbs
- Fred ma zwierzę, którym jest Tibbs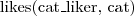 - (każdy) miłośnik kotów lubi (jakiegoś) kota
- (każdy) miłośnik kotów lubi (jakiegoś) kota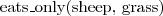 - (każda) owca je tylko trawę
- (każda) owca je tylko trawę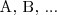 )
)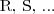 )
)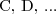 ); mogą nimi być:
); mogą nimi być: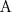 - pojęcie atomiczne
- pojęcie atomiczne - top concept, pojęcie uniwersalne oznaczające „wszystko”
- top concept, pojęcie uniwersalne oznaczające „wszystko”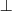 - bottom concept, pojęcie puste, oznaczające „nic”
- bottom concept, pojęcie puste, oznaczające „nic”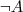 - negacja
- negacja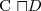 - koniunkcja
- koniunkcja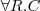 - kwantyfikator uniwersalny: „dla każdego”
- kwantyfikator uniwersalny: „dla każdego”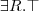 - kwantyfikator egzystencjalny/szczegółowy: „istnieje”
- kwantyfikator egzystencjalny/szczegółowy: „istnieje”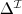 - niepustego zbioru, na który mapowane są symbole i relacje
- niepustego zbioru, na który mapowane są symbole i relacje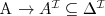
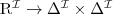
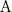
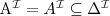
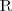
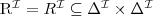

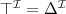
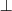
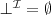
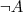
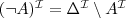
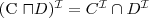
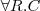
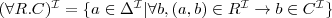
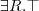
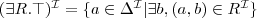

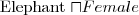
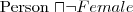
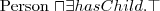
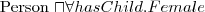
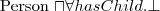
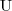 - suma :
- suma : 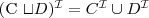
 - pełny kwantyfikator egzystencjalny :
- pełny kwantyfikator egzystencjalny : 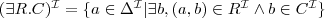
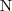 - ograniczenia liczbowe:
- ograniczenia liczbowe: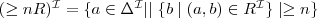
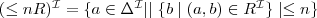
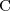 - negacja :
- negacja : 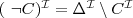
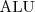
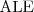
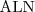
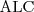 → odpowiada podzbiorowi logiki pierwszego rzędu ograniczonemu do formuł z dwoma zmiennymi
→ odpowiada podzbiorowi logiki pierwszego rzędu ograniczonemu do formuł z dwoma zmiennymi





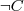
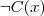
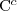 (dopełnienie zbioru)
(dopełnienie zbioru)
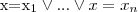

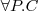
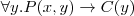
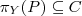
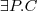
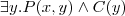
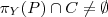 (Π - projekcja)
(Π - projekcja)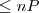
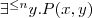
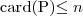 (card - liczność zbioru)
(card - liczność zbioru)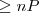
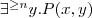
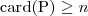

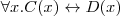
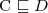
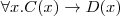
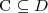
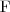 ograniczenia funkcyjne (np. ≤1hasMother)
ograniczenia funkcyjne (np. ≤1hasMother)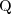 warunkowe ograniczenia liczbowe (np. ≥2hasChild.Doctor))
warunkowe ograniczenia liczbowe (np. ≥2hasChild.Doctor)) z użyciem instancji (e.g., {Italy})
z użyciem instancji (e.g., {Italy}) role odwrotne (np.
role odwrotne (np.  )
) przechodniość relacji
przechodniość relacji hierarchia relacji (e.g.,
hierarchia relacji (e.g., 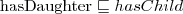 )
)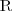 zawieranie się relacji: RoS ⊆ R, RoS ⊆
zawieranie się relacji: RoS ⊆ R, RoS ⊆ 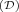 użycie typów danych w obrębie języka
użycie typów danych w obrębie języka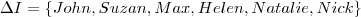 ,
,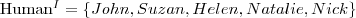 ,
, 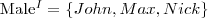 ,
, 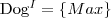 ,
, 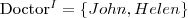 ,
, 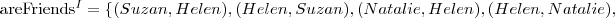
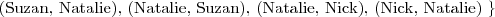 ,
,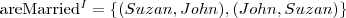 ,
, 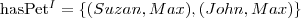 .
.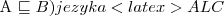 :
:
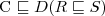
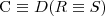
 mapuje każde pojecie na podzbiór dziedziny
mapuje każde pojecie na podzbiór dziedziny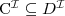 lub
lub 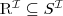
 lub
lub 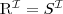
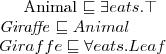
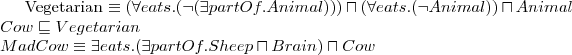
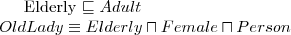
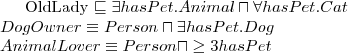
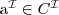
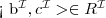



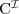 jest niepusty.
jest niepusty.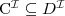 dla każdego modelu I terminologii T.
dla każdego modelu I terminologii T. dla każdego modelu I terminologii T.
dla każdego modelu I terminologii T.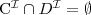 dla każdego modelu I terminologii T.
dla każdego modelu I terminologii T.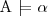 iff każda interpretacja spełniająca A spełnia również α.
iff każda interpretacja spełniająca A spełnia również α.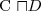 is subsumed by ⊥
is subsumed by ⊥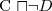 is unsatisfiable (this is used in tableau-based algorithms)
is unsatisfiable (this is used in tableau-based algorithms)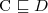 wtw. gdy wyrażenie
wtw. gdy wyrażenie 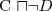 jest niespełnialne.
Schemat działania:
jest niespełnialne.
Schemat działania:
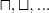 )
)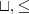 ) (w praktyce prowadzi to do przeszukiwania)
) (w praktyce prowadzi to do przeszukiwania)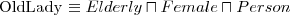
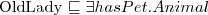

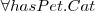
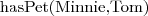 ,
,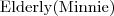 ,
,