Spis treści
Laboratorium 6 - Sztuczne sieci neuronowe
Ćwiczenia bazujące na materiałach Andrew Ng.
Przed zajęciami przejrzyj wykłady VIII i IX
Instructions in English.
Ćwiczenia do pobrania (files to download): Neural Networks
Lista i opis plików
- ex4.m - Skrypt pomagający przejść przez laboratorium
- ex4data1.mat - Dane uczące zawierające pismo odręczne
- ex4weights.mat - Parametry sieci neuronowej
- displayData.m - funkcja wizualizująca zbiór danych
- fmincg.m - Funkcja wyznaczająca minimum (podobna do fminunc)
- sigmoid.m - funkcja sigmoidalna
- computeNumericalGradient.m - Numerycznie oblicza gradienty
- checkNNGradients.m - Funkcja sprawdzajaca gradienty
- debugInitializeWeights.m - Funkcja inicjalizujaca wagi początkowe
- predict.m - Funkcja predykcji dla sieci neuronowej
 sigmoidGradient.m - Obliczanie gradientów dla funkcji sigmoidalnej
sigmoidGradient.m - Obliczanie gradientów dla funkcji sigmoidalnej- randInitializeWeights.m - Losowa inicjalizacja wag sieci neuronowej
 nnCostFunction.m - funkcja kosztu dla sieci neuronowej
nnCostFunction.m - funkcja kosztu dla sieci neuronowej
Rozgrzewka
Zanim zaczniemy właściwą część zajęć, poświeć chwilę na obejrzeniu jak działa prosta sieć neuronowa w akcji: http://playground.tensorflow.org/
Zastanów się co wpływa na jakość klasyfikacji:
- ilość neuronów w warstwie ukrytej?
- funkcja aktywacji neuronu?
- cechy, które podajemy na wejściu?
- ilość danych wejśćiowych?
- współczynnik regularyzacji lub learning rate?
- ilość warstw ukrytych?
Wstęp
Celem ćwiczeń laboratoryjnych jest nauczenie sieci neuronowej rozpoznawania cyfr. Sieć neuronowa będzie składać się z 3 warstw. Ilość neuronów w warstwie wyjściowej będzie równa ilości klasyfikowanych wzorców (czyli w naszym przypadku 10).
Struktura sieci neuronowej przedstawiona jest na rysunku poniżej. Pierwsza warstwa zawiera 400 perceptronów, warstwa ukryta zabiera 25 neuronów, a warstwa wyjściowa 10.
Funkcja kosztu
Uzupełnij plik nnCostFunction.m wyznaczając koszt i gradient dla sieci neuronowej.
Uwaga Macierz X, zawierająca zbiór uczący, zbudowana jest w taki sposób, że poszczególne elementy uczące znajdują się w wierszach. Aby dostać się do i-tego przykładu uczącego należy zatem odwołać się do niego w następujący sposób: X(i,:).
Uwaga Macierz X nie zawiera elementów biasu, dlatego w funkcji nnCostFunction.m konieczne jest dodanie tych elementów!
Uwaga Parametry 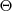 dla poszczególnych warstw sieci znajdują się w zmiennych Theta1 oraz Theta2. Theta1 ma rozmiar 25 x 401. Theta2 ma rozmiar 10 x 26.
dla poszczególnych warstw sieci znajdują się w zmiennych Theta1 oraz Theta2. Theta1 ma rozmiar 25 x 401. Theta2 ma rozmiar 10 x 26.
Wartość funkcji kosztu obliczany jest za pomocą wzoru:
![Equation $$J(\theta)= \frac{1}{m}\sum_{i=1}^{m}\sum_{k=1}^{K}\left [ -y_k^{(i)}log((h_\theta(x^{(i)}))_k)-(1-y_k^{(i)})log(1-(h_\theta(x^{(i)}))_k \right ]$$](/lib/exe/fetch.php?media=wiki:latex:/imgd652289d21bcbb2244795f6bd08fbc8a.png)
Gdzie 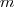 to ilość przykładów w zbiorze uczącym, a
to ilość przykładów w zbiorze uczącym, a 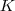 to ilość etykiet (w naszym przypadku 10).
to ilość etykiet (w naszym przypadku 10).
Uwaga Pamiętaj aby poprawnie obliczyć wartość 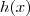 , która w przypadku sieci neuronowej polega na wymnożeniu współczynników wag Theta i danych wejściowych - zobacz rysunek powyżej.
, która w przypadku sieci neuronowej polega na wymnożeniu współczynników wag Theta i danych wejściowych - zobacz rysunek powyżej.
Uwaga Sieć neuronowa ma 10 neuronów w warstwie wyjściowej. Zatem wyjście sieci oznaczające, że rozpoznano np liczbę 3, będzie wyglądać następująco (cyfrę zero reprezentować będzie 10 indeks wektora y):
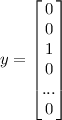
Sprawdź działanie funkcji za pomocą skrypty check.m. Uruchom skrypt ex4.m. Powinieneś zobaczyć koszt równy około 0.287629.
Funkcja kosztu z regularyzacją
Wartość funkcji kosztu obliczany jest za pomocą wzoru:
![Equation $$
J(\theta)= \frac{1}{m}\sum_{i=1}^{m}\sum_{k=1}^{K}\left [ -y_k^{(i)}log((h_\theta(x^{(i)}))_k)-(1-y_k^{(i)})log(1-(h_\theta(x^{(i)}))_k \right ] + R(\theta)
$$](/lib/exe/fetch.php?media=wiki:latex:/img7b9dd2cf64ec64b26e14db0b0cc961a4.png)
Gdzie
![Equation $$
R(\theta) = \frac{\lambda}{2m}\left [ \sum_{j=1}^{25}\sum_{k=1}^{400}(\Theta_{j,k}^{(1)})^2+\sum_{j=1}^{10}\sum_{k=1}^{25}(\Theta_{j,k}^{(2)})^2 \right ]
$$](/lib/exe/fetch.php?media=wiki:latex:/imgea4cbf53f7962a9feafc29737e1876dd.png)
Uwaga Pamiętaj, żeby we wzorze na remaskularyzację nie uwzględniać biasu.
Przetestuj działanie funkcji za pomocą skryptu check.m. Przetestuj działanie funkcji za pomocą skryptu ex4.m. Powinieneś otrzymać wynik funkcji kosztu na poziomie około 0.383770.
Gradient funkcji sigmoidalnej
Do wykonania następnego zadnia konieczne jest wyznaczenie gradientu funkcji sigmoidalnej. Uzupełnij plik sigmoidGradient.m. Gradient dla funkcji sigmoidalnej obliczany jest wg. wzoru:
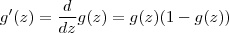
Sprawdź poprawność działania funkcji za pomocą skryptu check.m.
Backpropagation
 Dla każdego elementu t ze zbioru uczącego wykonaj następujące kroki (tutaj nie da się uniknąć pętli for t=1:m … end).
Dla każdego elementu t ze zbioru uczącego wykonaj następujące kroki (tutaj nie da się uniknąć pętli for t=1:m … end).
- Ustaw wartości perceptronów (warstwa wejściowa
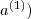 na t-ty element ze zbioru uczącego
na t-ty element ze zbioru uczącego 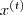 . Wykonaj propagacje wprzód (patrz rysunek pierwszy), obliczając poszczególne wartości dla warstw wewnętrznych (
. Wykonaj propagacje wprzód (patrz rysunek pierwszy), obliczając poszczególne wartości dla warstw wewnętrznych (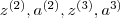 ). Pamiętaj o uwzględnieniu biasu w zmiennych
). Pamiętaj o uwzględnieniu biasu w zmiennych 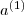 oraz
oraz 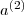 . Np. a_1 = [1; a_1].
. Np. a_1 = [1; a_1]. - Dla każdego neuronu z warstwy wyjściowej oblicz
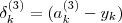
- Dla ukrytej warstwy
 , ustaw:
, ustaw:
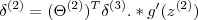
- Oblicz zakumulowany gradient dla danego elementu t. Pamiętaj żeby pominąć
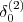 :
:
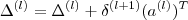
- Wyznacz niezregularyzowany gradient:
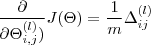
Uruchom skrypt ex4.m i sprawdź poprawność działania algorytmu. Sprawdź działanie algorytmu za pomocą skryptu check.m
Regularyzowane backpropagation
Regularyzacja gradientu polega na następującej modyfikacji wzoru:
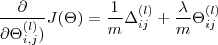
Uwaga Pamiętaj aby pominąć bias!
Przetestuj działanie algorytmu przy pomocy skryptu check.m oraz ex4.m.