This is an old revision of the document!
Modeling Games in GDL
The main goal of this class is to learn how to model turn games in a rule based language. After finishing the class, student should be able to model simple games and point out the difficulties related with this task.
1 Preliminaries
GDL (Game Description Language) is a language designed to describe turn games. It was created to be used in so called General Game Playing, a subdomain of the AI, focused on creating bots able to play in any game that can be formally described.
The class is based on a tutorial from Stanford and slides from the university in Dresden.
2 Modeling the World
There are two main approaches to model the world of the game:
coarse-grained — where every state of the game is a state in a giant state machine. Every unique state corresponds to one state in the machine. The state machine may grow quite impressive. Beside that state doesn't have any structure so is no really helpful if you want to exploit it to solve the problem in an intelligent manner.
fine-grained — state of the world is defined by so called
fluents, which can be treated as variables. The state here is structured (the current values of the fluents) which we may use.
GDL belongs to the fine-grained family, so there are:
fluents (actions made by the players are a special kind of fluent
game rules, which are represented by… rules
3 Example: Tic-Tac-Toe
We will show the basic features of the GDL on the example of the popular tic-tac-toe game.
Players
Let's start with players “nought” and “cross”. There is a special fact role just to do that:
role(nought)
role(cross)
Syntax is the same as in the Prolog (or Datalog) language with the only difference, that there is no dot at the end of the sentece. All constants start with a lower-cased letter and variables are upper-cased.
Fluents
Now we should define fluents that make up the game state. In a Tic-Tac-Toe game there are 29 fleunts:
1 fluent per every cell, telling if there is a cross (x) in the cell (9 fluents)
1 fluent per every cell, telling if there is a nought (o) in the cell (9 fluents)
1 fluent per every cell, telling if the cell is empty (blank - b) (9 fluents)
1 fluent per player, telling if it is his turn to play (2 fluents).
To define the fluents one uses the base facts:
Here :- reprenst implication ←. & is a logical and. In natural language the first line means: “if M and N represent cells' indexes, then there is a fluent for cell with (M, N) coordinates, telling there is a cross in it”. If we didn't use rules, we could write all the fluents by hand:
base(cell(1,1,x)) base(cell(1,1,o)) base(cell(1,1,b))
base(cell(1,2,x)) base(cell(1,2,o)) base(cell(1,2,b))
base(cell(1,3,x)) base(cell(1,3,o)) base(cell(1,3,b))
base(cell(2,1,x)) base(cell(2,1,o)) base(cell(2,1,b))
base(cell(2,2,x)) base(cell(2,2,o)) base(cell(2,2,b))
base(cell(2,3,x)) base(cell(2,3,o)) base(cell(2,3,b))
base(cell(3,1,x)) base(cell(3,1,o)) base(cell(3,1,b))
base(cell(3,2,x)) base(cell(3,2,o)) base(cell(3,2,b))
base(cell(3,3,x)) base(cell(3,3,o)) base(cell(3,3,b))
base(control(nought))
base(control(cross))
Rules in GDL have a one special feature: they can recurse, but they can't loop forever. More details here.
Available Actions
Now, we should model available actions, there are 20 of them here:
1 action per every cell, that the player puts the 'nought' in
1 action per every cell, that the player puts the 'cross' in
1 action noop per user, telling that player does do nothing
Thee noop action exists only in order to simulate the players' turns. When one player makes the action then the second one has to take the noop action.
In order to define an action we use the input predicate:
input(R, mark(M,N)) :- role(R) & index(M) & index(N)
input(R, noop) :- role(R)
The input predicates takes two arguments, first is the player, second is the action itself.
Legal Moves
Knowing the available actions, we have to define when the action is a legal move with a legal predicate. We use the true predicate to check if the fluent is true at the moment..
legal(W,mark(X,Y)) :-
true(cell(X,Y,b)) &
true(control(W))
legal(nought,noop) :-
true(control(cross))
legal(cross,noop) :-
true(control(nought))
In other words - player may mark a cell only if it is empty and it is his turn. If it is not his turn, he can only perform the 'noop' action.
Initial State
Now we have to define the initial state of the game (draw the empty board). The init predicate serves this purpose. For the tic-tac-toe every cell should be empty, and the nought player should play first.
init(cell(M,N,b)) :- index(M) & index(N)
init(control(nought))
State Changes
Now the most difficult part — how does the state evolve in the game. We assume that the new state is created after the very move and depends only on the previous state and actions made by the players. On could notice the frame problem occurring here. The etymology of the frame is the movie tape, where every frame differs in details from the previous one. Similarly here, we would like the next state to be exactly like the previous one except some changes made explicitly by the players. The problem is that in our case we have also to model lack of changes :(
To define the state evolution we use the next predicate, defining the fluent state in the next turn. The 'does' predicate check what actions were made by the players during the current turn.
next(cell(M,N,x)) :-
does(cross,mark(M,N)) &
true(cell(M,N,b))
next(cell(M,N,o)) :-
does(nought,mark(M,N)) &
true(cell(M,N,b))
next(cell(M,N,W)) :-
true(cell(M,N,W)) &
distinct(W,b)
next(cell(M,N,b)) :-
does(W,mark(J,K)) &
true(cell(M,N,b)) &
distinct(M,J)
next(cell(M,N,b)) :-
does(W,mark(J,K))
true(cell(M,N,b)) &
distinct(N,K)
next(control(nought)) :-
true(control(cross))
next(control(cross)) :-
true(control(nought))
The defined actions mean that:
if the cell is empty and the 'cross' player marked it then there will be a 'x' in this cell next turn
if the cell is empty and the 'nought' player marked it then there will be an 'o' in this cell next turn
if the cell wasn't empty (distinct checks equality of the arguments), then it will stay the same next turn
if the cell was empty and wasn't mark this turn, it will be still empty next turn (two rules!)
if the current turn belongs to the the 'nought' player, next will belong to the 'cross' player
if the current turn belongs to the the 'cross' player, next will belong to the 'nought' player
It's worth to note, that actions 3 and 4 are designed only to cope with the frame problem.
Game Ending Conditions
Every player knows that there are two ways to finish the game: make a line or fill all the available cells. Now we will check if there was a line made by the player.
The true(line(naught)) query will tell if there is a line made of the 'o's on the board.
Now we can define the ending conditions with the terminal predicate:
Game ends when:
The '~' operator means negation. Similarly to the Prolog it follows the closed world assumption, ie. sentence is false if can't prove otherwise. In GDL ther are additional restrictions we want worry about for now (more info here).
Winning Conditions
 Bots don't have feelings but we still should give them prize for the good game. And we do this with the
Bots don't have feelings but we still should give them prize for the good game. And we do this with the goal predicate:
goal(cross,100) :- line(x) & ~line(o)
goal(cross,50) :- ~line(x) & ~line(o)
goal(cross,0) :- ~line(x) & line(o)
goal(nought,100) :- ~line(x) & line(o)
goal(nought,50) :- ~line(x) & ~line(o)
goal(nought,0) :- line(x) & ~line(o)
According to the rules above winner gets 100 (so much win!), in case of tie only 50, and loser gets 0. We don't what this number represent but it has to be something good like cookies.
There is no arithmetics in GLD — numbers are only used to define indexes, prizes, time, etc.
Koniec
To by było na tyle, właśnie udało się zamodelować prostą grę w kółko i krzyżyk.
3.1 Zad 1
Weźmy przykładowy model jeszcze prostszej gry.
Odpowiedz na poniższe pytania:
jak wielu graczy występuje w grze?
jak wiele fluentów opisuje stan gry?
jak wiele jest dostępnych akcji?
ile akcji może wykonać gracz 'white' w początkowym stanie gry?
jak wiele fluentów jest prawdziwych w początkowym stanie gry?
załóżmy, że pierwszej turze gracz 'white' wykonał akcję 'a', a gracz 'black' akcję 'd'. Ile fluentów jest prawdziwych w drugiej turze?
jaka jest najmniejsza liczba kroków potrzebna do zakończenia gry?
czy gra zawsze się kończy? (czy mogłaby się zapętlić?)
3.2 Zad 2
Proszę zamodelować grę w 'krzyżyk i krzyżyk'. Podobnie jak w przypadku 'kółka i krzyżyk' mamy dziewięć pól, tym razem jednak obaj gracze stawiają krzyżyki. Przegrywa ten gracz, który pierwszy doprowadzi do powstania linii.
3.3 Zad 3
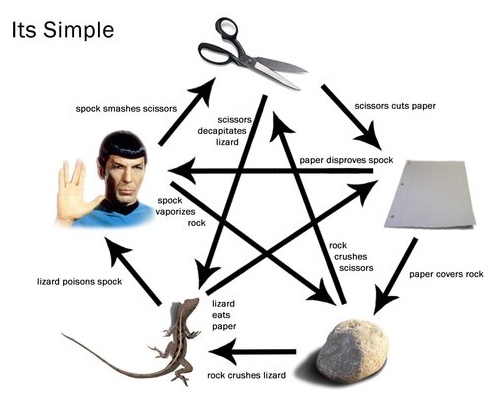 Proszę zamodelować grę w “kamień, papier, nożyce, spocka i jaszczurkę”. W razie problemów ze zrozumieniem reguł, proszę obejrzeć instrukcję video. Obrazek obok przedstawia użyteczną referencję. . Poćwiczyć można na żywo w sali, lub, jak na prawdziwego człowieka XXI wieku przystało, online....
Proszę zamodelować grę w “kamień, papier, nożyce, spocka i jaszczurkę”. W razie problemów ze zrozumieniem reguł, proszę obejrzeć instrukcję video. Obrazek obok przedstawia użyteczną referencję. . Poćwiczyć można na żywo w sali, lub, jak na prawdziwego człowieka XXI wieku przystało, online....
O ile wszystko, co zostało powyżej napisane, jest prawdą, o tyle większość systemów GGP nie wspiera reprezentacji w stylu Prolog. Na potrzeby wysyłania i zapisania wiedzy (reprezentowanej w sposób regułowy) powstał format KIF (Knowledge Interchange Format). Podobnie jak w przypadku PDDL, bazuje on na lispie i używa notacji prefixowej. Ponadto symbol :- zestępowany jest przez strzałkę ⇐, symbol koniunkcji & przez and, symbol negacji ~ przez not. Nazwy zmiennych poprzedzane są znakiem zapytania ?. Poniżej przedstawiony jest przykład translacji z wersji a'la Prolog:
do formatu KIF:
4.1 Zad 1
Dla każdej z poniższych par określ, czy wersja prefixowa, jest wiernym tłumaczeniem wersji Prologowej.
4.2 Zad 2
4.3 Zad 3
4.4 Zad 4
Przepisz modele 'kólka i krzyżyka', 'krzyżyka i krzyżyka' oraz 'papier, kamień, nożyce, spocka i jaszczurki' do postaci KIF.
5 Walidacja modeli
Poniższe instrukcje przygotowane są z myślą o laboratorium C2 316, gdzie każdy komputer ma Eclipse.
Proszę uruchomić Eclipse i następnie:
File → Import Project
Wybrać opcję importowania z repozytorium git
Jeżeli tej opcji nie ma (Eclipse jest za stare), to trzeba ręcznie sklonować repo i zaimportować projekt z katalogu. Reszta tutejszej instrukcji nie ma sensu

Wybrać opcję klonowania z zewnętrznego
URI-
Wybrać gałąź master
Wybrać jakiś rozsądny katalog dla projektu
Wybrać projekt ggp-base do zaimportowania
5.1 Dodanie gier do środowiska
W katalogu projektu proszę dostać się do ścieżki games/games i stworzyć tam trzy katalogi kolko-krzyzyk, krzyzyk-krzyzyk i spock. Każdy katalog powinien zawierać dwa pliki:
5.2 Walidacja gier
Z poziomu Eclipse proszę uruchomić aplikację Validator (rozwijana lista przy guziki play).
Validator, jak sama nazwa wskazuje, ma na celu sprawdzenie, czy dany model jest prawidłowym modelem GDL.
Ćwiczenia
W polu Repository wybrać Local Game Repository
W polu Game wybrać Tic-Tac-Toe
Wciśnąć przycisk Validate — program powinien pokazać same sukcesy
Powtórzyć to samo dla własnych modeli
Poprawić własne modele
Zdobyć kolejne sukcesy.
6 Zabawa
Z poziomu Eclipse proszę uruchomić aplikację Kiosk (rozwijana lista przy guziki play).
Ćwiczenia
W polu Opponent proszę wybrać SimpleMonteCarloPlayer
Wybrać jakąś znajomą grę
Wygrać!




