LAB: Praca z listami w Prologu (cz. 2)
1. Zadania z list do samodzielnego rozwiązania
Korzystając z wiedzy zdobytej w pierwszej części laboratorium z listami proszę rozwiązać następujące problemy:
zdefiniować predykat, powodujący usunięcie 3 ostatnich elementów listy L, w wyniku powstaje lista L1, użyć sklej.
zdefiniować predykat, powodujący usunięcie 3 pierwszych elementów listy L, w wyniku powstaje lista L1, użyć sklej.
zdefiniować predykat, powodujący usunięcie 3 pierwszych i ostatnich elementów listy L, w wyniku powstaje lista L2, użyć sklej.
zdefiniować parę komplementarnych predykatów nieparzysta(L) oraz parzysta(L) sprawdzajacych czy argument jest listą o odpowiednio nie/parzystej długości.
zdefiniować predykat palindrom(L), L jest palindromem, jeżeli czyta się tak samo od przodu i tyłu, np. [a,l,a], [m,a,d,a,m]. (podpowiedź: można nie/użyć odwroc.)
zdefiniować predykat
przesun(L1,L2), gdzie L2, jest przesuniętą rotacyjnie o jeden element L1, np.:
?- przesun([1,2,3,4,5,6,7,8],X),przesun(X,Y),przesun(Y,Z).
X = [2, 3, 4, 5, 6, 7, 8, 1]
Y = [3, 4, 5, 6, 7, 8, 1, 2]
Z = [4, 5, 6, 7, 8, 1, 2, 3]
zdefiniować predykat
przeloz(L1,L2), który zamienia listę liczb (max. 0-9), na listę słów:
?- przeloz([1,4,7],X).
X = [jeden, cztery, siedem] ;
?- przeloz(A,[dwa,osiem,zero]).
A = [2, 8, 0] ;
posługując się faktami:
znaczy(0,zero). znaczy(1,jeden).
znaczy(2,dwa). znaczy(3,trzy).
znaczy(4,cztery). znaczy(5,piec).
znaczy(6,szesc). znaczy(7,siedem).
znaczy(8,osiem). znaczy(9,dziewiec).
Podpowiedź: predykat ma być rekurencyjny.
zdefiniować predykat
podzbior(L,Z), który sprawdza, czy Z zawiera się w L, oraz wypisuje wszystkie możliwe podzbiory L (jeżeli Z jest niewiadoma).
?- podzbior([a,b,c],[c]).
Yes
?- podzbior([a,b,c],[a,c]).
Yes
?- podzbior([a,b,c],X).
X = [a, b, c] ;
X = [a, b] ;
X = [a, c] ;
X = [a] ;
X = [b, c] ;
X = [b] ;
X = [c] ;
X = []
zdefiniować predykat
podziel(L,L1,L2), który dzieli listę L, na dwa fragmenty L1 i L2, mniej więcej równej długości (z dokładnością do jednego el.), np.:
?- podziel([],X,Y).
X = []
Y = [] ;
?- podziel([1],X,Y).
X = [1]
Y = [] ;
?- podziel([1,2],X,Y).
X = [1]
Y = [2] ;
?- podziel([1,2,3],X,Y).
X = [1, 3]
Y = [2] ;
?- podziel([1,2,3,4],X,Y).
X = [1, 3]
Y = [2, 4] ;
?- podziel([1,2,3,4,5],X,Y).
X = [1, 3, 5]
Y = [2, 4] ;
?- podziel([1,2,3,4,5,6,7,8],X,Y).
X = [1, 3, 5, 7]
Y = [2, 4, 6, 8] ;
zdefiniować predykat
splaszcz, który zamienia dowolnie zagnieżdżoną listę, w listę płaską (której el. nie są listami). (podstawowe rozwiązanie działa bez nawrotów - nie należy naciskać
;)
?- splaszcz([[a],b,c],X).
X = [a, b, c]
?- splaszcz([[a],[b,[d]],c],X).
X = [a, b, d, c]
?- splaszcz([a,b,c],X).
X = [a, b, c]
?- splaszcz(a,X).
X = [a]
Napisz program który obliczy na jakie monety można rozmienić zadaną sumę pieniędzy.
Zdefiniuj nominały monet: np. moneta(1) oznacza monetę jednozłotową,
Predykat rozmieniający powinien mieć dwa argumenty: rozmien/2, gdzie pierwszy to kwota, a drugi lista nominałów monet na jakie można rozmienić kwotę; uwaga: predykat będzie niedeterministyczny.
2. Przechwytywanie wyników
Z Prologiem dostarczonych jest kilka predykatów przydatnych przy obróbce wyników wyszukiwania.
Predykat bagof/3, użyty jako bagof(X,P,L) buduje listę L, złożoną z takich X, że spełnione jest P.
Podobnie działa setof/3, jednak powstała lista jest posortowana i nie zawiera ew. duplikatów.
Specjalny operator ^ pozwala na modyfikowanie zapytania i jest równoważny kwantyfikacji egzystencjalnej, np. zakładając istnienie bazy faktów zdefiniowanej za pomocą predykatu a/2:
bagof(X,Y^a(X,Y),L) spowoduje znalezienie listy L na ktorej beda znajdować się wartości X niezależnie od tego jaką wartość przyjmuje Y (dokładnie jedno rozwiązanie).
bagof(X,a(X,Y),L) spowoduje znalezienie listy L na ktorej beda znajdować się wartości X dla konkretnej (znalezionej) wartości Y (wiele rozwiązań, lista dla każdej wartości Y).
 : składnia z ^ nie działa (w zainst. wersji SWI), jeżeli jest użyta jako cel w powłoce SWI - należy zdefiniować odpowiedni predykat jej używający w pliku.
: składnia z ^ nie działa (w zainst. wersji SWI), jeżeli jest użyta jako cel w powłoce SWI - należy zdefiniować odpowiedni predykat jej używający w pliku.
Predykat findall/3 wymusza wyszukanie wszystkich możliwych wyników.
Ćwiczenie:
Wczytać program z 1. zajęć rodzina1.pl
Sprawdzić działanie:
?- rodzic(X,robert).
?- bagof(X,rodzic(X,robert),L).
Sprawdzić działanie:
?- bagof(X,ojciec(tomek,X),L).
?- setof(X,ojciec(tomek,X),L).
Następnie:
?- bagof(X,Y^ojciec(X,Y),L).
?- setof(X,Y^ojciec(X,Y),L).
Oraz:
?- bagof(X,ojciec(X,Y),L).
?- findall(X,ojciec(X,Y),L).
3. Labirynt
Dany jest program poszukujacy drogi w labiryncie: maze.pl.
Proces poszukiwania uruchamiany jest za pomocą predykatu solve_maze/.
Głównym predykatem definiujacym algortym poszukiwania jest path/2.
Labirynt znajduje się na ponumerowanych polach.
Połączenia pomiędzy polami, którymi można przejść zdefiniowane są za pomocą predykatu connect/2.
Wejście do labiryntu oznaczone jest start, wyjście: finish.
Poniższy przykład definoiuje bardzo prosty labirynt.
connect(start,1).
connect(1,2).
connect(2,3).
connect(2,4).
connect(3,finish).
Ćwiczenie:
1. Przeanalizuj program maze.pl. Do czego służy predykat connected_to/2?
2. Napisz odpowiednie klauzule predykatu connect/2 dla labiryntu danego na rysunku poniżej oraz uruchom program poszukujący drogi.
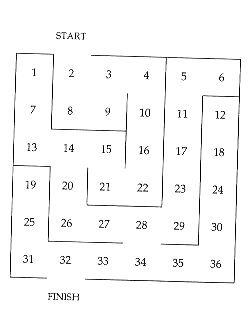
3. Zmodyfikuj labirynt, tak aby do wyjścia prowadziła więcej niż jedna droga. Czy solve_maze/0 znajdzie więcej niż jedną drogę? Czy path/2 znajdzie więcej niż jedną drogę?
4. Zagadka
Na blokach piramidek (patrz rysunki) należy umieścić cyfry od 1 do 9. W niebieskich rzędach cyfry muszą być różne, w żółtych - mogą się powtarzać, a w różowych - przynajmniej jedna powtórka jest obowiązkowa. Każda cyfra (poza umieszczonymi w podstawie) musi być sumą lub różnicą dwu cyfr znajdujących się bezpośrednio pod nią. Część liczb jest już na swoich miejscach. Napisz program w Prologu, który poda rozwiązania piramidek.
Wskazówka: Przeczytaj „helpa” do predykatu list_to_set/2. Może się okazać przydatny…
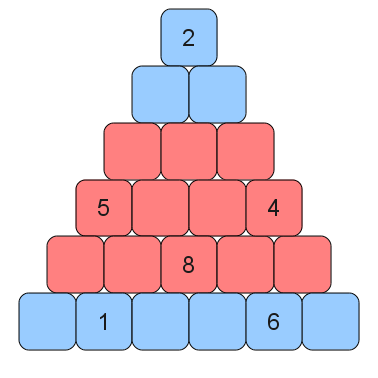
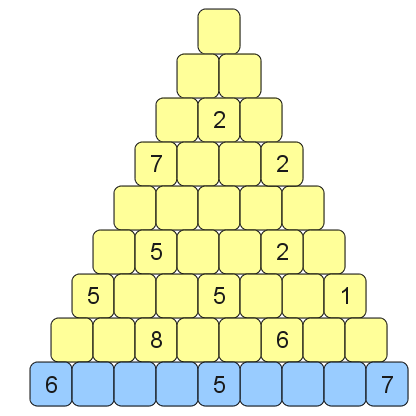
Komentarze
Z braku lepszego miejsca tutaj studenci wpisują komentarze natury ogólnej do tego lab. 
— Grzegorz J. Nalepa 2008/02/20 14:34
 : składnia z ^ nie działa (w zainst. wersji SWI), jeżeli jest użyta jako cel w powłoce SWI - należy zdefiniować odpowiedni predykat jej używający w pliku.
: składnia z ^ nie działa (w zainst. wersji SWI), jeżeli jest użyta jako cel w powłoce SWI - należy zdefiniować odpowiedni predykat jej używający w pliku.


