Celem ćwiczenia jest zapoznanie się z możliwościami wykorzystania Prologu do planowania tras przejazdu oraz poznanie technik poszukiwania ścieżek w grafach i ich implementacji w Prologu.

Modelem przestrzeni poszukiwań dla planowania tras przejazdu jest graf.

Graf to twór matematyczny składający się ze zbioru wierzchołków V (ang. nodes, vertices) oraz zbioru krawędzi E (ang. links, edges).

Najprostsza definicja grafu mówi, że graf to para postaci G=(V,E), gdzie V jest zbiorem węzłów a E ⊆ V×V jest zbiorem łączących je krawędzi.

Model ten reprezentuje schmatycznie mapę, gdzie w zależności od poziomu abstrakcji węzły mogą np. reprezentować miasta, a krawędzie - łączące je drogi, lub też węzły mogą reprezentować skrzyżowania ulic a krawędzie ulice (lub ich odcinki).

Zapoznaj się, lub raczej przypomnij sobie podstawowe wiadomości o grafach.

• Grafy (pl.wikipedia.org),
• Graph (ew.wikipedia.org).

Pamiętaj, że krawędź grafu może być skierowana (modeluje przejazd tylko w jedną stronę; np. ulica jednokierunkowa) lub nieskierowanym (modeluje przejazd w obie strony; np. ulica dwukierunkowa).

Odpowiednio, graf może byc grafem skierowanym, nieskierownym lub mieszanym.

Ponadto, z każdą krawędzią może być związany koszt przejazdu (odległość, czas).

Jeżeli dwa węzły grafu połączone są więcej niż jedną krawędzią, krawędzie te muszą być etykietowane dla umożliwienia ich rozróżnienia.

Zadanie planowania tras przejazdu to zadanie polegające na wyznaczeniu drogi łączącej zadany punkt początkowy i pożądany punk docelowy.

Zwykle dążymy do wyznaczenia trasy najkrótszej, najszybszej lub o najniższym koszcie.

Modelem zadania planowania trasy jest poszukiwanie ścieżki w grafie.

Zadania planowania trasy definiowane jest jako:

P = (v_I, v_G, V, E)

gdzie v_I to zadany węzeł początkowy, v_G to zadany węzeł docelowy, a V oraz E definiują graf (przestrzeń poszukiwań).

Rozwiązaniem zadania planowania trasy jest ciąg krawędzi e_1, e_2,…,e_n, taki, że:

• {e_1, e_2,…,e_n} ⊆ E,
• e_1 zaczyna się węźle v_I,
• krawędź e_i kończy się w węźle będącym początkiem krawędzi e_i+1,
• krawędź e_n kończy się w węźle v_G.

Powyższy ciąg krawędzi tworzy ścieżkę stanowiącą plan przejazdu.

Zwykle wymaga się aby każdy węzeł leżący na ścieżce przejazdu odwiedzany był tylko raz (brak cykli).

Zanych jest wiele algorytmów przeszukiwania grafów.

Zapoznaj się z podstawowymi algorytmami:

• Algorytmy przeszykiwania w głąb i wszerz,
• Klasycznym algorytme Dijkstry i //problemem najkrótszej ścieżki//,
• Elegancką prezentacją algorytmu Dijkstry.

Plan dopuszczalny to plan stanowiący rozwiązanie (ścieżka łącząca węzeł początkowy i docelowy) i ew. spełniający zadane ograniczenia (np. długości, omijania wybranych węzłów zabronionych, przechodzenia przez zadane węzły wymagające odwiedzenia, etc. Plan ten nie musi być 'najlepszy'.

Plan optymalny to plan najlepszy w sensie wybranego kryterium, np.

• plan zawierający najmniejszą liczbę węzłów,
• plan realizujący najkrótszą trasę,
• plan o najtańszej trasie przejazdu,
• plan pozwalający na najszybszy przejazd.

W Prologu można reprezentowac grafy na kilka sposobów.

Najprostszą i efektywną metodą jest zadeklarowanie połączeń pomiędzy węzłami grafu w postaci faktów w Prologu.

Rozważmy następujący graf:

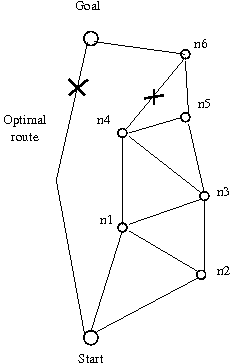
Przykład grafu - model połączeń drogowych (.pdf)

W grafie tym istnieje jedna ścieżka optymalna (lewa krawędź) oraz wiele ścieżek dopuszczalnych przechodzących przez węzły n1-n6.

Reprezentacja tego grafy w Prologu ma postać:

d(s,g).
d(s,n1).
d(s,n2).
d(n1,n2).
d(n1,n4).
d(n1,n3).
d(n2,n3).
d(n3,n4).
d(n3,n5).
d(n4,n5).
d(n4,n6).
d(n5,n6).
d(n6,g).

Jak widać, każda krawędź zapisywana jest w postaci relacji d(<węzeł_poczatkowy>,<węzeł_końcowy>).

W przykładowym grafie istnieje 13 krawędzi. Zgodnie z deklaracją w Prologu, są to krawędzie skierowane (dlaczego

Aby zadeklarować możliwość przejazdu w obie strony, należy zdefiniować domknięcie symetryczne relacji połączenie d/2.

%%% domknięcie symetryczne relacji d/2 
     przejazd(X,Y):- d(X,Y).
     przejazd(X,Y):- d(Y,X).

Tak więc, każda krawędź umożliwia przejazd w obie strony.

1. Przerysuj pokazany graf na kartce papieru.
2. Znajdź - wspomagając się rysunkiem kilka mozliwych alternatywnych tras przejazdu; zaznacz je na rysunku.
3. Spróbuj wyznaczyć wszystkie różne trasy przejazdu (nie zawierające cykli); ile ich jest?

Rozważmy najprostszy program realizujący zadanie poszukiwania tras przejazdu:

%%% domknięcie tranzytywne relacji przejazd

     szukaj_trasy(Cel,Cel,Trasa,Trasa):- !.

     szukaj_trasy(Miasto,Cel,Robocza,Trasa):- 

          przejazd(Miasto,NoweMiasto),

          not(member(NoweMiasto,Robocza)),

          szukaj_trasy(NoweMiasto,Cel,[NoweMiasto|Robocza],Trasa).

Predykat szukaj_trasy/4 ma 4 parametry:

• aktualny węzeł (Miasto),
• węzeł docelowy (Cel),
• cząstkową trasę aktualną (Robocza),
• trasę docelową (Trasa).

Pierwszy wariant definiuje zakończenie poszukiwań: gdy znajdziemy się w weżle docelowym, trasa Robocza staje się docelową.

Drugi wariant definiuje sposób szukania trasy:

• będąc w węźle Miasto, znajdź NoweMiasto do którego jest bezpośrednie połączenie (uzywając predykatu przejazd/2,
• sprawdź, czy nie było juz odwiedzane ( not(member(NoweMiasto,Robocza)) ),
• jeżeli tak, zostanie wymuszony nawrót; jeżeli nie, próbuj dalej i w tym celu
• zaktualizuj trasę roboczą dokładając NoweMiasto i kontynuuj szukanie z tego miejsca.

Zauważ, że:

• trasy reprezentowane sa jako listy,
• konstruowana ścieżka wydłuża się w miarę szukania; dokładane są nowe miasta,
• konstruowane sa wszystkie warianty planu - dzięki mechanizmowi nawrotów w Prologu,
• żaden plan nie będzie zawierał cykli.

1. Uruchom podany program dla przykładowego grafu; jak zainicjować parametry?
2. Zadaj w jakiej kolejności wystepują miasta na znalezionych trasach. Dlaczego?
3. Wygeneruj przykładowy plan rozwiązania,
4. Wygeneruj wszystkie możliwe plany i policz je.

Aby ułatwic uruchamianie programu wyposażymy go w klauzulę inicjującą:

%%% inicjacja szukania

     plan(Start,Cel,Trasa):-

          szukaj_trasy(Cel,Start,[Cel],Trasa).                           

Zauważ, że Start i Cel zamieniły sie miejscami. Dlaczego?

Aby wyznaczyć automatycznie wszystkie plany uzupełnimy program o klauzulę:

%%% Find all plans from 's' to 'g'.
     fap(Plans) :- findall(Trasa, plan(s,g,Trasa),Plans).

Aby wyznaczyć automatycznie wszystkie plany i zapisać je do pamięci uzupełnimy program o klauzulę:

%%% Find all plans and assert; p(<plan>).
     fap-assert:- plan(s,g,Plan), assert(p(Plan)), fail.
     fap-assert.

Jaka to konstrukcja? Na czym polega jej działanie?

Pełny program znajdziesz tutaj: plan-robust-count.pl

1. Przeanalizuj elementy i działanie programu.
2. Jaka jest kolejność węzłów w wygenerowanych planach?
3. W jakiej kolejności (w jakim kierunku) odbywa się rzeczywista genetacja planów?
4. Policz ile jest planów dopuszczalnych (programowo) i porównaj wynik z rozwiązaniem ręcznym.
5. Zmodyfikuj program tak, aby dla każdego planu wyznaczał jego długość (ilość odwiedzanych węzłów).
6. Zastanów się jak zeralizować (a może nawet spróbuj) analogiczny program w Twoim ulubionym języku programowania (np. Java, C++, Python). Porónaj naklad pracy z kodowaniem w Prologu.