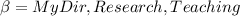Introduction to Description Logics
| Last verification: | 20180914 |
| Tools required for this lab: | – |
Introduction
1 Description Logics Intro
In Introduction to ontologies you have learnt basic ideas about ontologies.
Ontologies consist of classes, properties and individuals.
Classes describe sets of objects.
Properties describe relations between classes and attributes of classes.
Individuals are instances of classes linked with other individuals by properties.
Classes may be organized into hierarchies.
Properties may be organized into hierarchies.
There are object properties and data properties.
Properties have domains and ranges.
The above information can be expressed in RDF Schema which is a simple ontology language for the Semantic Web.
However, more complex ontologies require more expressive language. For example:
How to say that the range of a property hasChildren is Person when applied to a person and Elephant when applied to an elephant?
How to say that all instances of person have a mother that is also a person, or that persons have exactly 2 parents?
How to say that isPartOf is a transitive property, that hasPart is the inverse of isPartOf or that touches is symmetrical?
In this lab, you will get to know more advanced ontologies based on Description Logics (DL).
You will learn the DL languages and understand how OWL corresponds to selected DL.
1.1 Description Logics Basics
DL are a family of Knowledge Representation formalisms
they describe world of interest by means of concepts and relations between them
they provide formal semantics and inference services
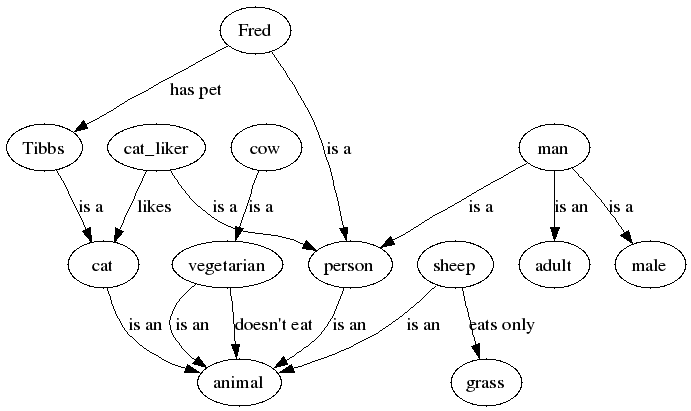
Fig.1. Exemplary graph.
1.1.1 Examples of DL expressions
Assertions about individuals
concept assertions e.g.
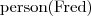
- Fred is a person
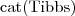
Tibbs is a cat
role assertions e.g.
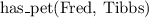
- Fred has a pet which is Tibbs
Statements about concepts
concept definitions (necessary and sufficient conditions) e.g.
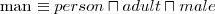
- A man is an adult male person
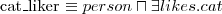
- A cat liker is a person and there exists a cat that he/she likes
relations between concepts e.g.
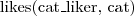
- (every) cat liker likes a cat
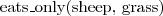
- (every) sheep eats only grass
axioms e.g.
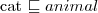
a cat is an animal (hierarchy of concepts)
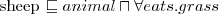
a sheep is an animal which eats only grass (it's a
necessary but not sufficient condition)
1.1.2 Relation to First Order Logic
| Description | DL syntax | FOL syntax | Set algebra |
| A man is a male and an adult and a person |  |  |  |
| A newspaper is a broadsheet or a tabloid |  |  |  |
| Everything a vegetarian eats is not an animal | 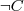 | 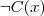 | 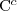 (complement of set) (complement of set) |
| EU countries are: Germany, France, …, Poland |  | 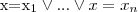 |  |
| An old lady has only cats | 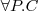 | 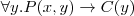 | 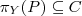 |
| A dog owner has some dog(s) | 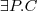 | 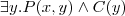 | 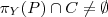 (Π - projection) (Π - projection) |
A reasonable man has maximum 1 woman  | 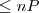 | 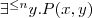 | 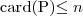 (card - cardinality) (card - cardinality) |
| An animal lover has minimun 3 pets | 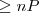 | 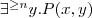 | 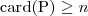 |
| A kid is the same as a young person |  | 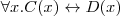 |  |
| Every cat is an animal | 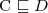 | 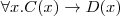 | 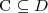 |
1.2 Description Logic Languages
elementary descriptions are atomic concepts and atomic roles
complex descriptions built from them inductively with concept constructors
Description Languages are distinguished by the constructors they provide
1.2.1 Basic DL language
1.2.1 More Description Logics
1.2.2 Nominals in TBox
1.2.3 Language extensions
Base DL is ALC (≈ALUE).
Additional letters indicate language extensions:
regarding concept constructors
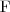
for functional number restrictions (e.g., ≤1
hasMother)
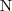
for number restrictions (graded modalities, e.g., ≥2
hasChild, ≤
3hasChild)
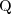
for qualified number restrictions (graded modalities, e.g., ≥2
hasChild.Doctor))
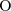
for nominals/singleton classes (e.g., {Italy})
regarding role constructors
additional role axioms
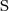
Role transitivity - often used for

extended with transitive roles

Role hierarchy (e.g.,
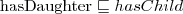
)
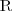
Complex role inclusions: RoS ⊆ R, RoS ⊆ S
other
Use of datatype properties, data values or data types
Expressiveness of the language influence its reasoning complexity: DL complexity navigator
1.3 Knowledge Representation systems based on DL
A Knowledge Representation System based on DL provides means to set up a knowledge base, to manipulate it and reason about it
The knowledge base consists of
TBox - terminology, intensional representation
ABox - assertions about individuals, extensional representation
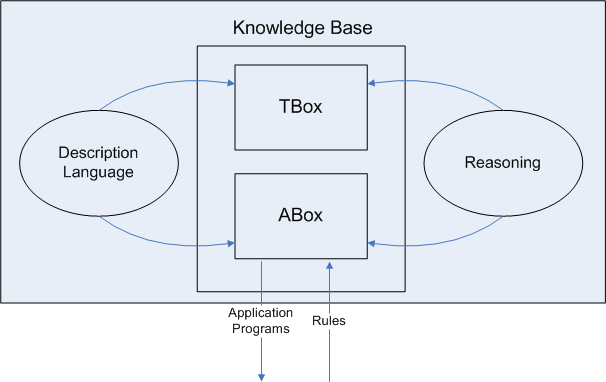
1.3.1 Terminologies (TBox)
TBox semantics:
TBox Example
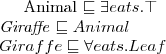
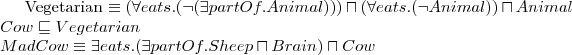
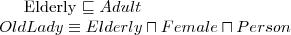
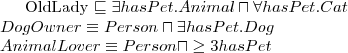
1.3.2 World Description (ABox)
an ABox contains extensional knowledge about the domain of interest (individuals)
concept assertions, e.g. C(a)
role assertions, R(b,c)
ABox semantics
ABox Example

1.3.3 Unique name assumption and Closed-world assumption
There are two features of Description Logic that are not shared by most other data description formalisms: DL does not make the Unique name assumption (UNA) or the Closed-world assumption (CWA):
Not having UNA means that two concepts with different names may be allowed by some inference to be shown to be equivalent.
Not having CWA, or rather having the Open world assumption (OWA) means that lack of knowledge of a fact does not immediately imply knowledge of the negation of a fact.
1.4 OWL (Web Ontology Language) and DL
1.4.1 OWL and DL Syntax Compared

OWL and DL constructs
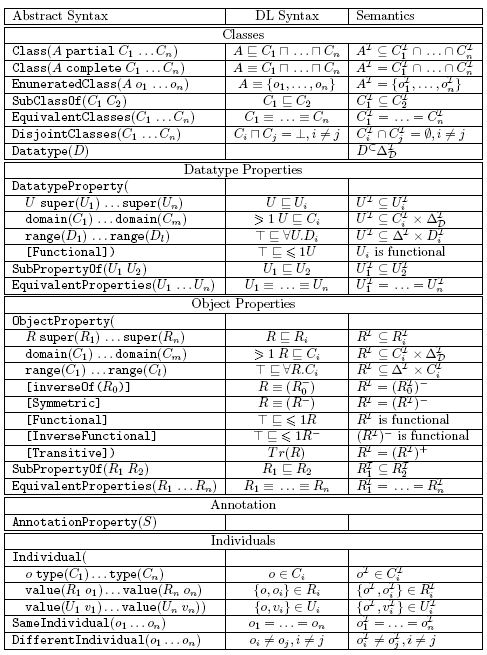
OWL and DL axioms
Example
Pizza ontology fragment in DL:
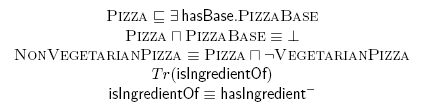
The same fragment in OWL Abstract syntax:
Namespace(p = <http://example.com/pizzas.owl#>)
Ontology( <http://example.com/pizzas.owl#>
Class(p:Pizza partial
restriction(p:hasBase someValuesFrom(p:PizzaBase)))
DisjointClasses(p:Pizza p:PizzaBase)
Class(p:NonVegetarianPizza complete
intersectionOf(p:Pizza complementOf(p:VegetarianPizza)))
ObjectProperty(p:isIngredientOf Transitive
inverseOf(p:hasIngredient))
)
1.4.2 OWL - Abstract syntax
Using the tables above translate the following class descriptions into DL syntax:
Ontology(
Class(pp:male partial)
Class(pp:adult partial)
Class(pp:elderly partial pp:adult)
Class(pp:pet complete restriction(pp:is_pet_of someValuesFrom(owl:Thing)))
Class(pp:animal partial restriction(pp:eats someValuesFrom(owl:Thing)))
/* Vegetarians do not eat animals or parts of animals */
Class(pp:vegetarian complete
intersectionOf(pp:animal
restriction(pp:eats allValuesFrom(complementOf(pp:animal)))
restriction(pp:eats
allValuesFrom(complementOf(restriction(pp:part_of
someValuesFrom(pp:animal)))))))
DisjointClasses(pp:dog pp:cat)
ObjectProperty(pp:eaten_by)
ObjectProperty(pp:eats inverseOf(pp:eaten_by) domain(pp:animal))
SubPropertyOf(pp:has_pet pp:likes)
Individual(pp:Tom type(owl:Thing))
Individual(pp:Tibbs type(pp:cat))
1.4.3 OWL - XML syntax
<owl:Class>
<owl:intersectionOf rdf:parseType="collection">
<owl:Class rdf:about="#Person"/>
<owl:Restriction>
<owl:onProperty rdf:resource="#hasChild"/>
<owl:toClass>
<owl:unionOf rdf:parseType="collection">
<owl:Class rdf:about="#Doctor"/>
<owl:Restriction>
<owl:onProperty rdf:resource="#hasChild"/>
<owl:hasClass rdf:resource="#Doctor"/>
</owl:Restriction>
</owl:unionOf>
</owl:toClass>
</owl:Restriction>
</owl:intersectionOf>
</owl:Class>
1.4.4 Species of OWL
OWL 1:
OWL Full is union of OWL syntax and RDF
OWL DL is restricted to FOL fragment
Has standard (First Order) model theoretic semantics
Equivalent to SHOIN(D): role transitivity(S) + role hierarchy (H) + nominals (O) + inverse (I) + number restrictions (N) + datatype properties, data values or data types (D) = SHOIN(D)
OWL Lite is „simpler” subset of OWL DL
OWL 2:
-
OWL 2 EL
OWL 2 QL
OWL 2 RL
and OWL 2 DL?
2 Lab instructions
2.1 Description Logics - TBox and ABox
Here we will do some Description Logics „with pen and paper”.

Let's check if you understand this difference properly: Take your ontology from one of the previous labs (WebProtege or Protege). Identify which statements belong to Terminology (TBox) and World Description (ABox). Put them in the report divided into two sections: TBox and ABox.
NOTE: You don't have to translate the statements into DL. Just select parts of the existing file.
2.2 Description Logics - Reasoning

Let's consider a simple Knowledge Base about directories and files:
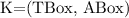
. Which of the following statements could be reasoned from
and why? (you can write solutions by hand, take a photo and put it in the report)
-
-
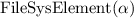
, where

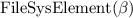
, where
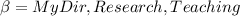
If you want to know more
Lecture:
Description Logics:

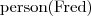 - Fred is a person
- Fred is a person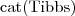 Tibbs is a cat
Tibbs is a cat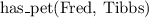 - Fred has a pet which is Tibbs
- Fred has a pet which is Tibbs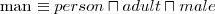 - A man is an adult male person
- A man is an adult male person 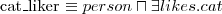 - A cat liker is a person and there exists a cat that he/she likes
- A cat liker is a person and there exists a cat that he/she likes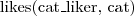 - (every) cat liker likes a cat
- (every) cat liker likes a cat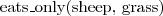 - (every) sheep eats only grass
- (every) sheep eats only grass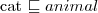 a cat is an animal (hierarchy of concepts)
a cat is an animal (hierarchy of concepts)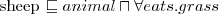 a sheep is an animal which eats only grass (it's a necessary but not sufficient condition)
a sheep is an animal which eats only grass (it's a necessary but not sufficient condition)





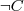
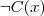
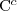 (complement of set)
(complement of set)
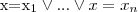

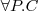
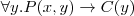
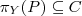
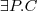
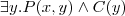
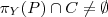 (Π - projection)
(Π - projection)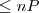
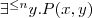
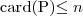 (card - cardinality)
(card - cardinality)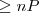
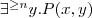
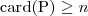

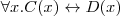
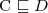
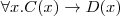
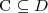
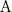
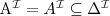
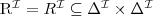

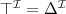
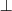
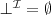
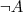
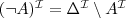
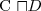
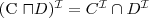
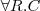
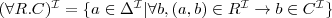
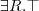
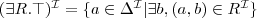

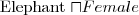
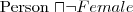
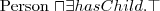
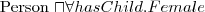
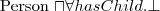
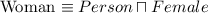
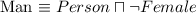
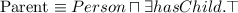
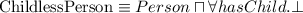
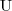 - union
- union 
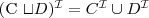
 - full existential quantification
- full existential quantification 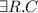

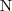 - number restrictions:
- number restrictions: 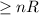
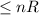
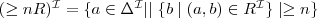
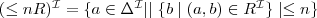
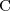 - negation
- negation 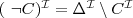
![LaTeX \mathcal{AL} [ \mathcal{U}][ \mathcal{E} ][\mathcal{N} ][\mathcal{C} ]](/lib/exe/fetch.php?media=wiki:latex:/img99b799b4d5ddcd9782d4ebfc1036c87e.png)
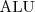 ,
, 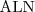 ,
, 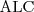
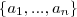 (semantics:
(semantics: 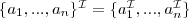 )
)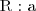 (semantics:
(semantics: 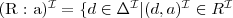 )
)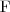 for functional number restrictions (e.g., ≤1hasMother)
for functional number restrictions (e.g., ≤1hasMother) for qualified number restrictions (graded modalities, e.g., ≥2hasChild.Doctor))
for qualified number restrictions (graded modalities, e.g., ≥2hasChild.Doctor))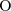 for nominals/singleton classes (e.g., {Italy})
for nominals/singleton classes (e.g., {Italy})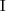 for inverse roles (e.g.,
for inverse roles (e.g.,  )
)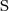 Role transitivity - often used for
Role transitivity - often used for  extended with transitive roles
extended with transitive roles Role hierarchy (e.g.,
Role hierarchy (e.g., 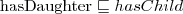 )
)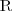 Complex role inclusions: RoS ⊆ R, RoS ⊆ S
Complex role inclusions: RoS ⊆ R, RoS ⊆ S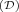 Use of datatype properties, data values or data types
Use of datatype properties, data values or data types
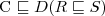 or
or 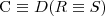
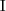 maps each concept name to a subset of the domain
maps each concept name to a subset of the domain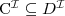 or
or 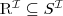
 or
or 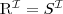
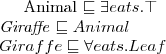
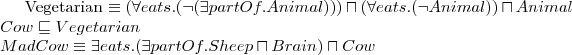
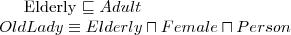
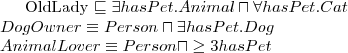
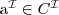
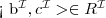



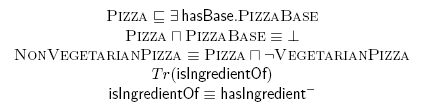
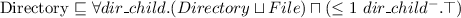
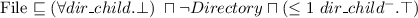

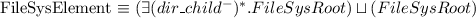
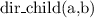
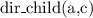
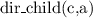
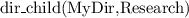
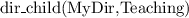
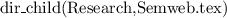
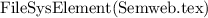

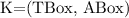 . Which of the following statements could be reasoned from
. Which of the following statements could be reasoned from 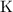 and why? (you can write solutions by hand, take a photo and put it in the report)
and why? (you can write solutions by hand, take a photo and put it in the report)
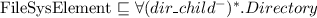
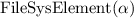 , where
, where 
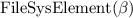 , where
, where