Wstęp
Na tych laboratoriach poznacie algorytm Monte Carlo Tree Search oraz zastosowanie go w poznanym już frameworku GVG-AI.
Metoda Monte Carlo
Jako, że Monte Carlo Tree Search powstało jako rozwinięcie powstałej już wcześniej metody Monte Carlo, najpierw przyjrzyjmy się pierwowzorowi.
Czym jest ta metoda
Metoda Monte Carlo jest szeroko stosowana w bardzo wielu dziedzinach. Pomaga rozwiązać zadania, które są trudne do rozwiązania z wykorzystaniem metod analitycznych i daje całkiem niezłe wyniki.
Najprościej przedstawić zasadę działania metody Monte Carlo opierając się na prostym przykładzie. Problem, który można w przybliżeniu rozwiązać z tej metody, to obliczenie liczby 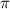 . Wiemy, że pole koła wyznaczamy wzorem
. Wiemy, że pole koła wyznaczamy wzorem 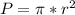 . Przez proste przekształcenia można uzyskać wzór
. Przez proste przekształcenia można uzyskać wzór 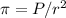 . Jesteśmy w stanie wyznaczyć promień takiego koła, ale trudniej już z jego polem. Rozwiązanie metodą Monte Carlo wygląda następująco:
. Jesteśmy w stanie wyznaczyć promień takiego koła, ale trudniej już z jego polem. Rozwiązanie metodą Monte Carlo wygląda następująco:
wyznaczamy kwadrat, w który jest wpisane wspomniane koło i wyznaczamy jego pole;
losujemy dostatecznie dużą ilość punktów leżących w kwadracie. Im więcej punktów, tym większa dokładność metody (ważne, by wartości dość równomiernie pokrywały kwadrat);
dla każdego punktu, korzystając z równania koła, sprawdzamy czy punkt leży w kole;
stosunek punktów leżących w kole do wszystkich punktów mnożymy przez pole kwadratu, co daje przybliżone pole koła.
Opierając się na podanym przykładzie, ogólną zasadę użycia metody Monte Carlo można przedstawić tak:
określamy dziedzinę problemu;
losujemy wartości z dziedziny starając się równomiernie wybierać zgodnie z rozkładem odpowiadającym dziedzinie;
testujemy wylosowane punkty zgodnie z typem zadania;
liczymy prawdopodobieństwo wyników pozytywnych i wykorzystujemy je do rozwiązania problemu.
Wykorzystanie w grach
Monte Carlo z powodzeniem wykorzystuje się również w grach. Wzorując się na powyższym schemacie:
dziedziną są dostępne akcje w danym stanie gry
akcje przeważnie mają takie samo prawdopodobieństwo na wystąpienie
testem tutaj może być symulacja losowej rozgrywki wykonanej po danym ruchu, a wynikiem rezultat tej symulacji. Dla każdego ruchu wykonujemy wiele symulacji, a wynik uśredniamy. Podobnie jak przy wyznaczaniu liczby
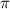
, im więcej takich, tym dokładniejszy rezultat
wynikiem działania algorytmu w tym problemie będzie wybór ruchu o największym średnim wyniku
Wykorzystanie w GVG
Stworzymy tutaj prostego bota opartego o metodę Monte Carlo. Ponieważ jest to już coś więcej niż proste losowanie akcji, jak w bocie z poprzednich laboratoriów, rozbijemy nasz program na kilka klas.
Najpierw zdefiniujmy klasę reprezentującą abstrakcyjny stan gry. Przechowuje ona informacje o rezultatach symulacji wykonanych w danym stanie gry oraz stanowi interfejs do wykorzystywanego frameworku.
- StateSpace.java
package monteCarlo.core;
import java.util.List;
public abstract class StateSpace<T> {
List<StateSpace<T>> children;
double score;
int simulationCount;
public T action;
public static long timeout;
public StateSpace<T> parent;
public abstract boolean gameEnd();
public abstract List<T> getActions();
public abstract StateSpace<T> makeSpace(T action);
public abstract double sim();
@Override
public String toString() {
return score + " " + simulationCount;
}
}
Kolejna klasa jest już implementacją Monte Carlo. Wykorzystuje ona powyższą klasę StateSpace. Posiada dwie publiczne metody:
sim() – przeprowadza jedną symulację i aktualizuje przechowywany stan gry o wyniki symulacji;
best() – zwraca akcję, która na podstawie przeprowadzonych symulacji dała najlepszy wynik.
- MC.java
package monteCarlo.core;
import java.util.*;
/**
* T, to typ akcji na jakiej pracuje algorytm
*/
public class MC<T> {
protected StateSpace<T> root;
protected Random random = new Random();
public MC(StateSpace<T> root) {
this.root = root;
}
public void sim(long timeout) {
root.timeout = timeout;
// metodą `select` wybierz ruch do przeprowadzenia symulacji
// uruchom symulację, zachowaj wynik
// zaktualizuj informację o ilości przeprowadzonych symulacji i wyniku
}
protected StateSpace<T> select(StateSpace<T> node) {
// zainicjalizuj węzeł metodą `expand` jeśli jeszcze to nie miało miejsca
// wybierz losowe dziecko węzła
}
protected void expand(StateSpace<T> node) {
// pobierz dostępne akcje węzła
// stwórz listę dzieci
// dla każdej dostępnej akcji stwórz dziecko i dodaj je do listy
}
public T best() {
// wybierz dziecko o najlepszym stosunku wygranych i zwróć jego akcję
}
}
Poniższa klasa jest implementacją abstrakcyjnego stanu gry tak, by można go było wykorzystać z GVG. Najtrudniejszym fragmentem jest symulacja. Ponieważ GVG narzuca nam dość rygorystyczne ograniczenia czasowe (odpowiedź musi przyjść w przeciągu 40 ms), musimy ograniczyć głębokość na jaką schodzimy w symulacjach i dalej opierać się na jakiejś heurystyce. W tej implementacji taką heurystyką jest liczba punktów w stanie, do jakiego udało się zejść.
Uwagi do implementacji deepSim:
- GVG_StateSpace.java
package monteCarlo.gvg;
import core.game.StateObservation;
import monteCarlo.core.StateSpace;
import ontology.Types;
import java.util.ArrayList;
import java.util.List;
import java.util.Random;
public class GVG_StateSpace extends StateSpace<Types.ACTIONS> {
private StateObservation state;
private Random random = new Random();
private GVG_StateSpace(StateObservation state, Types.ACTIONS action, GVG_StateSpace parent) {
this.action = action;
this.state = state;
this.parent = parent;
if (parent != null)
this.timeout = parent.timeout;
}
public GVG_StateSpace(StateObservation stateObs, Types.ACTIONS actions) {
this(stateObs, actions, null);
}
@Override
public boolean gameEnd() {
// pobierz informację ze StateObservation
}
@Override
public List<Types.ACTIONS> getActions() {
// pobierz informację ze StateObservation
}
@Override
public StateSpace<Types.ACTIONS> makeSpace(Types.ACTIONS action) {
// stwórz kopię obecnego stanu gry
// na kopię nanieś akcję
// zwróć nową instancję GVG_StateSpace ze sotwrzoną kopią i akcją z argumentu i `this` jako rodzicem
}
@Override
public double sim() {
// zwróć wynik głębokiej symulacji na kopii obecnego stanu, np dla 7 zagłębień
}
private double deepSim(StateObservation copy, int depth) {
// jeżeli czas się zakończył lub osiągnięto stan końca gry lub zagłębiono się wystarczająco
// pobierz wynik gry
// pobierz zwycięzcę
// gdy jest nim gracz, to zwiększ wynik o dużą wartość
// jeśli gracz jest przegrywem, zmniejsz wynik o dużą wartość
// jeśli gracz zdyskwalifikowany, to zmniejsz wynik o dużą, dużą wartość (nielegalny ruch)
// zwróć uzyskany wynik
// w innym przypadku
// pobierz dostępne akcje
// wylosuj następną i zaaplikuj na stanie gry
// wykonaj symulację na zaaplikowanym stanie dla zmniejszonego licznika zagłębienia
}
}
Dalej mamy już ostatnią klasę. Jest to znany nam agent. Jego zadaniem jest wykorzystanie zaimplementowanej przez nas metody Monte Carlo do wyboru najbardziej obiecującego ruchu.
Uwaga! Podając limity czasowe, proszę mieć na względzie, że symulacja zajmuje trochę czasu, więc trzeba odjąć od dostępnego czasu kilka milisekund potrzebnych na wykonanie jednej symulacji. Zawsze lepiej żeby bot nie wykorzystał całego czasu z powodu przeszacowania, niż został zdyskwalifikowany przez niedoszacowanie potrzebnego czasu.
- Agent.java
package monteCarlo;
import core.game.StateObservation;
import core.player.AbstractPlayer;
import monteCarlo.core.MC;
import monteCarlo.gvg.GVG_StateSpace;
import ontology.Types;
import tools.ElapsedCpuTimer;
public class Agent extends AbstractPlayer {
public Agent(StateObservation stateObs, ElapsedCpuTimer elapsedTimer) {
}
@Override
public Types.ACTIONS act(StateObservation stateObs, ElapsedCpuTimer elapsedTimer) {
// stwórz symulator MC podając implementację StateSpace odpowiednią dla GVG
// dopóki wystarczy czasu
// wykonaj kolejną symulację podając jako timeout obecną chwilę plus maksymalny czas trwania symulacji
// zwróć ruch, który dał najlepsze wyniki przy symulacji
}
}
Monte Carlo Tree Search
Metoda Monte Carlo Tree Search (często nazywana MCTS) jest modyfikacją poznanej już metody Monte Carlo.
O ile metoda Monte Carlo wybiera ruchy do symulacji w sposób losowy, niezależnie od dotychczasowych wyników, o tyle MCTS preferuje wybór stanów, które do danego momentu dawały najlepsze rezultaty. Jednak ograniczenie się jedynie do tego kryterium prowadziło by do rozwijania jedynie tych gałęzi, które przy pierwszych próbach dały dobre wyniki. Metoda czasem wybiera gałęzie miej obiecujące, ponieważ może się okazać że pośród nich jest ruch pozwalający na zwycięstwo, lecz wcześniej nie dostrzeżony.
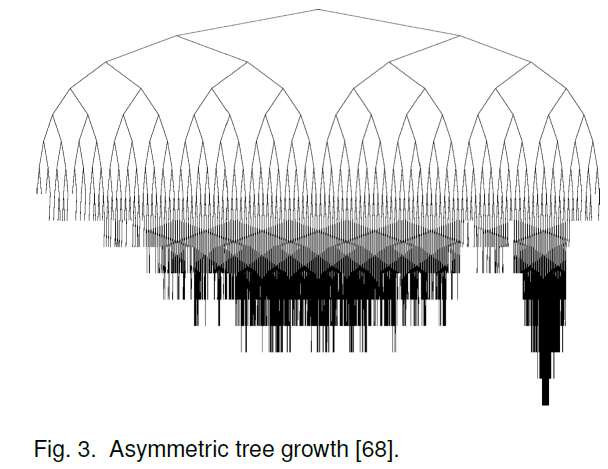
Poza tym w MCTS nie przechowujemy tylko stanów następnych od aktualnego. W tej metodzie istotnym jest przechowywanie coraz to kolejnych stanów, które podlegają symulacji powoli rozwijając drzewo stanu gry. Ze względu na preferowanie stanów dających największe nadzieje na wygraną, ich poddrzewa są najbardziej rozwinięte.
Kolejną różnicą względem podstawowego MC jest sposób wybierania ostatecznego ruchu. Tutaj nie wartościuje się ruchów pod względem stosunku wygranych do ilości symulacji, a jedynie liczbę symulacji. Jednak, z uwagi na to, że najczęściej symulowane są ruchy o największym stosunku wygranych, nie jest to zasada tak absurdalna, na jaką może wyglądać.
Zarys algorytmu
Jak już wspomniano, MCTS wykorzystuje zmodyfikowaną regułę wyboru węzła, które poddaje się symulacji. Algorytm powinien wybierać najbardziej obiecujące węzły (czyli eksploatować drzewo gry), lecz musi też poszukiwać innych ruchów, które również mogą okazać się obiecujące (eksploracja). Jedną regułą starającą się utrzymać równowagę między eksploatacją, a eksploracją jest UCT (artykuł na Wikipedii). Podana jest ona wzorem
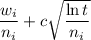
, gdzie 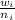 , to stosunek wygranych
, to stosunek wygranych 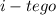 dziecka do ilości symulacji w nim przeprowadzonych;
dziecka do ilości symulacji w nim przeprowadzonych; 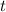 , to łączna liczba symulacji przeprowadzonych w aktualnie rozpatrywanym węźle, a
, to łączna liczba symulacji przeprowadzonych w aktualnie rozpatrywanym węźle, a  , to współczynnik eksploracji, zazwyczaj stosuje się wartość
, to współczynnik eksploracji, zazwyczaj stosuje się wartość 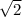 .
.
Metoda opiera się na czterech podstawowych operacjach:
wybór: poczynając od korzenia drzewa, stosując regułę UTC wybieraj kolejne węzły aż dojdziesz do liścia drzewa. Ponieważ stosowanie UTC na węzłach nie poddanych symulacji dało by dzielenie przez zero, zawsze wybieramy jeden z takich węzłów, o ile takie są;
rozrost: dla wybranego w poprzednim kroku węzła, o ile nie kończy on gry, utwórz jego dzieci potomne i wybierz jeden z nich; w innym wypadku pozostaw wybrany obecny węzeł
symulacja: na wybranym przy rozroście węźle, operacja identyczna z przebiegającą w metodzie Monte Carlo;
propagacja wstecz: wynik symulacji jest aktualizowany w górę drzewa gry.
Wykorzystanie w GVG
Aby uwydatnić fakt, że Monte Carlo Tree Search jest rozszerzeniem metody Monte Carlo, jej implementację przygotujemy tworząc klasę, która dziedziczy po przygotowanej powyżej klasie MC (rozszerza ją).
- MCTS.java
package monteCarlo.core;
import java.util.*;
public class MCTS<T> extends MC<T> {
public MCTS(StateSpace<T> root) {
super(root);
}
@Override
protected void update(StateSpace<T> selected, double score) {
// użyj metody z klasy bazowej, by zaktualizować stan
// jeżeli stan ma rodzica
// zaktualizuj rodzica
}
@Override
protected StateSpace<T> select(final StateSpace<T> node) {
// jeżeli dzieci nie są zainicjalizowane
// użyj metody bazowej i zwróć rezultat
// jeżeli stan nie ma dzieci
// zwróć obecny stan
// z pośród dzieci wybierz te, które daje najmniejszy rezultat z wywołania metody `metric`
// wybrane dziecko przekaż do metody `select` i zwróć rezultat
}
private double metric(StateSpace<T> parent, StateSpace<T> child) {
// jeżeli dziecko nie wykonało symulacji
// zwróć `Double.MAX_VALUE`
// zwróć wynik wg reguły UCT
}
}
Jak widać, metoda MCTS niewiele się różni od klasycznego Monte Carlo. Główną zmianą jest zmodyfikowana metoda wyboru węzła, zgodnie z podaną wcześniej regułą UCT. Drugą modyfikacją jest sposób aktualizacji węzłów. Wynika to jedynie z tego, że MCTS dokonuje ekspansji węzłów wgłąb, podczas gdy klasyczna metoda przegląda jedynie kolejne ruchy.
Pozostaje już tylko dopisać klasę, która wykorzystuje nasz mowy algorytm.
- Agent.java
package monteCarlo;
import core.game.StateObservation;
import core.player.AbstractPlayer;
import monteCarlo.core.MC;
import monteCarlo.gvg.GVG_StateSpace;
import ontology.Types;
import tools.ElapsedCpuTimer;
public class Agent extends AbstractPlayer {
public Agent(StateObservation stateObs, ElapsedCpuTimer elapsedTimer) {
}
@Override
public Types.ACTIONS act(StateObservation stateObs, ElapsedCpuTimer elapsedTimer) {
// stwórz symulator MC podając implementację StateSpace odpowiednią dla GVG
// dopóki wystarczy czasu
// wykonaj kolejną symulację podając jako timeout obecną chwilę plus maksymalny czas trwania symulacji
// zwróć ruch, który dał najlepsze wyniki przy symulacji
}
}
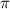 . Wiemy, że pole koła wyznaczamy wzorem
. Wiemy, że pole koła wyznaczamy wzorem 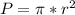 . Przez proste przekształcenia można uzyskać wzór
. Przez proste przekształcenia można uzyskać wzór 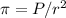 . Jesteśmy w stanie wyznaczyć promień takiego koła, ale trudniej już z jego polem. Rozwiązanie metodą Monte Carlo wygląda następująco:
. Jesteśmy w stanie wyznaczyć promień takiego koła, ale trudniej już z jego polem. Rozwiązanie metodą Monte Carlo wygląda następująco:

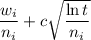
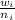 , to stosunek wygranych
, to stosunek wygranych 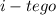 dziecka do ilości symulacji w nim przeprowadzonych;
dziecka do ilości symulacji w nim przeprowadzonych; 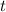 , to łączna liczba symulacji przeprowadzonych w aktualnie rozpatrywanym węźle, a
, to łączna liczba symulacji przeprowadzonych w aktualnie rozpatrywanym węźle, a  , to współczynnik eksploracji, zazwyczaj stosuje się wartość
, to współczynnik eksploracji, zazwyczaj stosuje się wartość 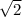 .
.