Constraint Programming: Wprowadzenie
Programowanie z ograniczeniami (ang. Constraint Programming, dalej nazywane CSP) jest deklaratywnym paradygmatem programowania, skupionym na modelowaniu problemu i wskazaniu wymagań (ograniczeń) stawianych jego rozwiązaniom. Do obowiązków programisty należy:
zamodelowanie problemu poprzez zdefiniowanie zmiennych o odpowiedniych dziedzinach,
zdefiniowanie ograniczeń, które określają dozwolone wartości zmiennych w rozwiązaniu
[opcjonalne] podanie kryterium oceny rozwiązania, np. minimalizacja długości trasy w problemie komiwojażera
[opcjonalne] sprecyzowanie procesu przeszukiwania przestrzeni możliwych rozwiązań.
Poniższe laboratoria mają za zadanie przedstawić motywacje oraz podstawowe techniki programowania CSP.
Przykład zastosowania
Przypuścmy, że pracujemy jako kelner w restauracji, która leży w pobliżu trwającej akurat konferencji informatyków zajmujących się optymalizacją dyskretną. Jest to bardzo niewdzięczna praca – przydarzają nam się różne nieprzyjemne przygody, takie jak ta opisana w poniższym komiksie:
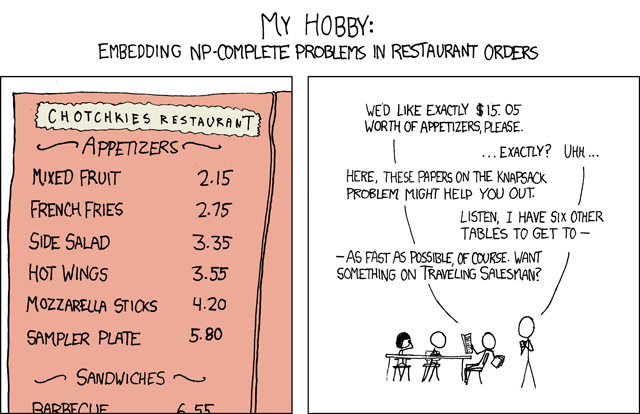
Sytuacja byłaby beznadziejna, ale na szczęście jest CSP. W dalszej części laboratorium będziemy modelować i rozwiązywać problem przedstawiony w komiksie.
Oprogramowanie
Do ściągnięcia:
Sala 316 ma już zainstalowane wszystkie potrzebne narzędzia. Jeżeli właśnie w niej siedzisz, możesz pominąć tę sekcję :)
Wybór wersji nowszej ma wady:
nie testowana na borgu (możesz być pierwsz(-y/-a), który tego dokona)
nie powstała jeszcze oficjalna dokumentacja dla tej wersji
i zalety:
zostało usuniętych wiele ograniczeń, który w duży stopniu utrudniały modelowanie
ma nowe funkcjonalności, użyteczne, gdyby ktoś się chciał zając tematem bardziej poważnie
IDE stało się bardziej profesjonalne
Instalacja:
Ściągnięte archiwa zawierają skompilowane już pliki binarne. Instalacja sprowadza się do rozpakowania plików. W przypadku paczki zawierającej solver rozsądne jest wywołanie skryptu SETUP, który przygotowuje środowisko do działania. W przypadku paczki zawierającej IDE, uruchamia się ono poprzez uruchomienie skryptu MiniZincIDE.sh. Po pierwszym uruchomieniu może być konieczne wskazanie ściezki do katalogu z solverem.
Aby IDE zadziałało na serwerze borg, należy do katalogu lib skopiować bibliotekę z archiwum: libqt5network.so.5.zip
Rozwiązanie problemu
Napisanie prostego programu w języku MiniZinc sprowadza się do czterech kroków.
1. Krok pierwszy: zmienne decyzyjne
Chcemy ustalić z czego ma składać się zamówienie, zatem potrzebujemy wiedzieć, ile razy ma zostać zamówione każde danie z osobna. Każda zmienna ma opisywać ile egzemplarzy danego dania zamówiono, powinna być więc typu liczby całkowitej (zakładamy, że nie można zamówić połowy dania). W MiniZinc zapiszemy to następująco (słowo kluczowe varwskazuje na zmienne decyzyjne):
var int: fruit;
var int: fries;
var int: salad;
var int: wings;
var int: sticks;
var int: sampler;
2. Krok drugi: ograniczenia
Jesteśmy przekonani, że nie da się zamówić ujemnej liczby dań, zatem wprowadzamy odpowiednie ograniczenia korzystając ze słowa kluczowego constraint:
constraint fruit >= 0;
constraint fries >= 0;
constraint salad >= 0;
constraint wings >= 0;
constraint sticks >= 0;
constraint sampler >= 0;
Ponadto wiemy, że suma kosztów zamówień ma być równa pewnej liczbie. Na razie będziemy używać jedynie liczb całkowitych i po prostu wszystkie ceny pomnożymy przez 100.
constraint fruit*215 + fries*275 + salad*335 + wings*355 + sticks*420 + sampler*580 == 1505;
3. Krok trzeci: cel
Szukamy takiego zamówienie, które spełnia (ang. satisfies) zadane ograniczenia. Słowo kluczowe solve oznacza moment, w których wybierany jest cel programu.
solve satisfy;
4. Wypisanie wyniku
Na koniec definiujemy, jak ma wyglądać wynik działania programu - służy do tego słowo kluczowe output:
output ["fruit:", show(fruit), "\t fries:", show(fries),
"\t salad:", show(salad), "\t wings:", show(wings),
"\t sticks:", show(sticks), "\t sampler:", show(sampler)];
Uruchomienie programu
Wszystkie powyższe linijki należy skopiować w danej kolejności do pliku z rozszerzeniem 
.mzn . Następnie w katalogu z plikiem, należy wykonać:
. Następnie w katalogu z plikiem, należy wykonać:
mzn-g12fd <nazwa_pliku>
lub
mzn-g12fd --all-solutions <nazwa_pliku>
jeżeli nie chcemy, by solver zatrzymał się pierwszym możliwym rozwiązaniu. W IDE można to wszystko „wyklikać” we względnie intuicyjny sposób (menu na górze → run, configuration → print all solutions).
Należy zadbać, żeby katalog bin solvera był na liście ściezek PATH:
export PATH=$PATH:<solver_dir/bin>
Napiwek 50%
Komiks twierdzi, że dostaniemy napiwek, jeżeli zdołamy stworzyć rozwiązanie ogólne. Napiwki są przydatne, zatem bierzemy się do roboty i parametryzujemy nasz problem.
1. Krok pierwszy: parametry
Najpierw ustalamy, ile pozycji zawiera menu i do jakiej liczby ma się równać koszt zamówienia. Brak słówka var sugeruje, że te wartości są niezmienne.
int: menu_length = 6;
int: money_limit = 1505;
Następnie posłużymy się tablicami w celu opisania zawartości menu. Każda tablica ma ustalony zakres indeksów i typ swoich elementów.
array[1..menu_length] of int: menu_prices = [215, 275, 335, 355, 420, 580];
array[1..menu_length] of string: menu_names = ["fruit", "fries", "salad", "wings", "sticks", "sampler"];
2. Krok drugi: definicja zmiennych
W wersji za napiwek liczba zmiennych również jest sparametryzowana – jest ich tyle samo, ile pozycji w menu.
array[1..menu_length] of var int: order;
3. Krok trzeci: ograniczenia
Liczba ograniczeń również zależy od rozmiarów menu. Aby je zdefiniować, posłużymy się funkcjami agregującymi: forall — dołącza wszystkie ograniczenia w tablicy, sum — sumuje liczby zawarte w tablicy. Notacja [array[i]*2 | i in 1..array_length] jest nazywana array comprehension i należy ją rozumieć jako wyrażenie przetwarzające elementy z jednej tablicy (1..array_length) na nową tablicę zawierającą elementy po lewej stronie |.
constraint forall([order[i] >= 0 | i in 1..menu_length]);
constraint sum([order[i] * menu_prices[i] | i in 1..menu_length]) == money_limit;
4. Krok czwarty: cel
5. Krok piąty: wypisanie wyniku
Aby wypisać wynik, również posłużymy się notacją array comprehension. Operator '++' łączy napisy, funkcja show przekształca liczbę w napis.
output [menu_names[i] ++ ": " ++ show(order[i]) ++ "\n" | i in 1..menu_length];
Uruchomienie kodu
Przebiega bez zmian. Proszę uruchomić program i zainkasować 50% z wyimaginowanej sumy pieniędzy.
Słabym elementem naszej dotychczasowej pracy jest zapisywanie wszystkich parametrów wewnątrz programu — przy zmianie menu musielibyśmy zmieniać program, co nie jest szczególnie ogólne i być może ten napiwek to nam się jeszcze do końca nie należy. Aby poradzić sobie z tym problemem, MiniZinc może wczytywać problemy z zewnętrznych plików. Proszę stworzyć plik o rozszerzeniu .dzn i zawartości:
menu_length = 6;
money_limit = 1505;
menu_prices = [215, 275, 335, 355, 420,580];
menu_names = ["fruit", "fries", "salad", "wings", "sticks", "sampler"];
Następnie proszę usunąć z programu wartości parametrów, zostawiając jedynie ich deklaracje, np. w miejsce linijki int: menu_length = 6; ma się znaleźć jedynie int: menu_length;.
Uruchamianie programu
Z poziomu konsoli należy wpisać:
mzn-g12fd -d <plik.dzn> <plik.mzn>
W IDE należy mieć otwarty plik .dzn i należy go wybrać jako Data file w zakładce Configuration.
Problem portfelowy
Dotychczas nasz cel był zdefiniowany jedynie jako satisfy — istnieją jeszcze dwa inne rodzaje celów: maximize <wyrażenie> oraz minimize wyrażenie, które odpowiednio poszukują rozwiązań, które maksymalizują/minimalizują wartość wyrażenia, np.
solve minimize sum(order);
znajdzie takie zamówienie, które spełnia wymagane ograniczenia i zawiera jak najmniej dań.
Ćwiczenie
Proszę dodać do programu kolejny parametr o nazwie yumyum_factors. Będzie to tablica liczb całkowitych, które wskazują jak bardzo dana pozycja w menu jest smaczna (im większy współczynnik yumyum, tym smaczniejsze danie).
Poszukujemy takiego rozwiązania, który maksymalizuję sumę wartości yumyum zamiówionych dań,
Należy zadbać, aby koszt zamówienia nie musiał być równy wartości money_limit, ale mógł być również od niego mniejszy.
