LAB: Przeszukiwanie grafów i planowanie tras przejazdu
Celem ćwiczenia jest zapoznanie się z możliwościami wykorzystania technik sztucznej inteligencji do planowania tras przejazdu oraz poznanie technik poszukiwania ścieżek w grafach.
1 Do przygotowania
2 Wprowadzenie
Modelem przestrzeni poszukiwań dla planowania tras przejazdu jest graf.
Graf to twór matematyczny składający się ze zbioru wierzchołków V (ang. nodes, vertices) oraz zbioru krawędzi E (ang. links, edges).
Najprostsza definicja grafu mówi, że graf to para postaci G=(V,E), gdzie V jest zbiorem węzłów a E ⊆ V×V jest zbiorem łączących je krawędzi.
Model ten reprezentuje schematycznie mapę, gdzie w zależności od poziomu abstrakcji węzły mogą np. reprezentować miasta, a krawędzie - łączące je drogi, lub też węzły mogą reprezentować skrzyżowania ulic a krawędzie ulice (lub ich odcinki).
Zapoznaj się, lub raczej przypomnij sobie  podstawowe wiadomości o grafach.
podstawowe wiadomości o grafach.
Pamiętaj, że krawędź grafu może być skierowana (modeluje przejazd tylko w jedną stronę; np. ulica jednokierunkowa) lub nieskierowanym (modeluje przejazd w obie strony; np. ulica dwukierunkowa).
Odpowiednio, graf może być grafem skierowanym, nieskierowanym lub mieszanym.
Ponadto, z każdą krawędzią może być związany koszt przejazdu (odległość, czas).
Jeżeli dwa węzły grafu połączone są więcej niż jedną krawędzią, krawędzie te muszą być etykietowane dla umożliwienia ich rozróżnienia.
3 Poszukiwanie ścieżek
Zadanie planowania tras przejazdu to zadanie polegające na wyznaczeniu drogi łączącej zadany punkt początkowy i pożądany punk docelowy.
Zwykle dążymy do wyznaczenia trasy najkrótszej, najszybszej lub o najniższym koszcie.
Modelem zadania planowania trasy jest poszukiwanie ścieżki w grafie.
Zadania planowania trasy definiowane jest jako:
P = (v_I, v_G, V, E)
gdzie v_I to zadany węzeł początkowy, v_G to zadany węzeł docelowy, a V oraz E definiują graf (przestrzeń poszukiwań).
Rozwiązaniem zadania planowania trasy jest ciąg krawędzi e_1, e_2,…,e_n, taki, że:
{e_1, e_2,…,e_n} ⊆ E,
e_1 zaczyna się węźle v_I,
krawędź e_i kończy się w węźle będącym początkiem krawędzi e_i+1,
krawędź e_n kończy się w węźle v_G.
Powyższy ciąg krawędzi tworzy ścieżkę stanowiącą plan przejazdu.
Zwykle wymaga się aby każdy węzeł leżący na ścieżce przejazdu odwiedzany był tylko raz (brak cykli).
Znanych jest wiele algorytmów przeszukiwania grafów, zarówno w obszarze teorii grafów, badań operacyjnych jak i sztucznej inteligencji.
Algorytmy z obszaru sztucznej inteligencji wyróżniają się tym, że:
często korzystają z heurystyk odległościowych (np. opartych na oszacowaniu odległości Euklidesowej i wg metryki ulicznej),
pozwalają na uwzględnianie dodatkowych ograniczeń, np. węzłów zabronionych,
pozwalają na przeszukiwanie przestrzeni o bardzo dużych rozmiarach,
pozwalają na przeszukiwanie przestrzeni zadanych niejawnie (nowe węzły lub stany pojawiają się w wyniku wywołania funkcji generującej).
Zapoznaj się z podstawowymi algorytmami:
Plan dopuszczalny to plan stanowiący rozwiązanie (ścieżka łącząca węzeł początkowy i docelowy) i ew. spełniający zadane ograniczenia (np. długości, omijania wybranych węzłów zabronionych, przechodzenia przez zadane węzły wymagające odwiedzenia, etc. Plan ten nie musi być 'najlepszy'.
Plan optymalny to plan najlepszy w sensie wybranego kryterium, np.
plan zawierający najmniejszą liczbę węzłów,
plan realizujący najkrótszą trasę,
plan o najtańszej trasie przejazdu,
plan pozwalający na najszybszy przejazd.
4 Wyszukiwanie najkrótszej ścieżki
-
Dla algorytmów heurystycznych zdefiniuj heurystykę wpisując w pole My heuristic wartość „dx”.
Jakie są najpopularniejsze heurystyki dla wyszukiwania na płaszczyźnie?
Przeczytaj
artykuł i wprowadź opisane w nim heurystyki obserwując zmiany działania algorytmu (aby wykonać operację pierwiastkowania wpisz
Math.sqrt(dx)).
Zadania
Przed wykonaniem zadań należy odświeżyć stronę aby przywrócić jej stan początkowy.
Zadanie 1
Po wygenerowaniu siatki, naciśnij przycisk
Build test, plansza powinna wyglądać następująco:

Używając algorytmu wyszukaj najkrótszą ścieżkę, niezależnie od jego rodzaju powinna ona przebiegać następująco:
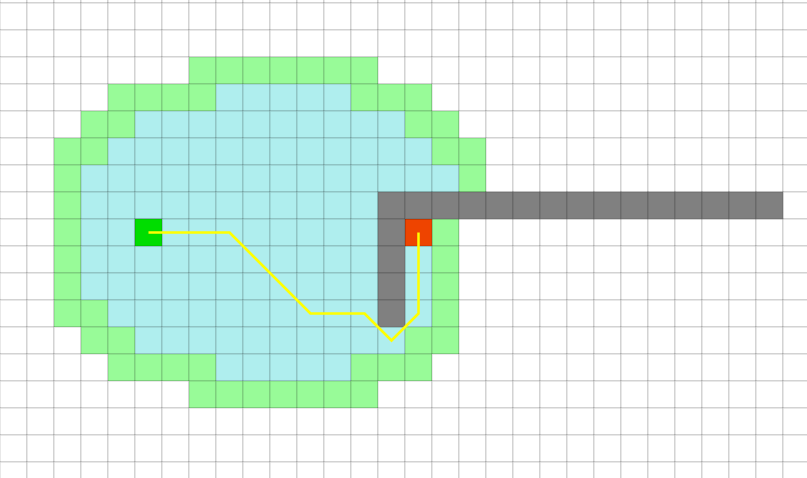
Zmodyfikuj heurystykę algorytmu
Best-First Search i
A* w taki sposób aby znaleziona ścieżka przebiegała nad dłuższą krawędzią - tak jak na poniższym rysunku:

Zadanie 2
Zamodeluj planszę jak na rysunku poniżej
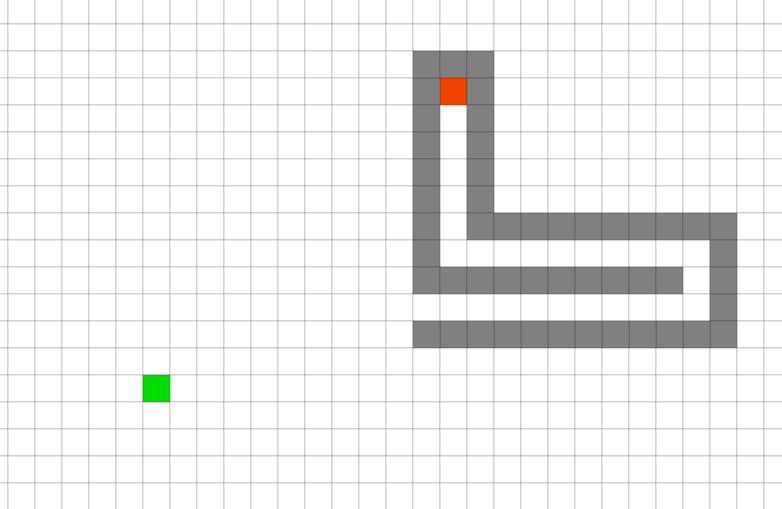
Spróbuj wymyślić heurystykę która pozwoli na jak najszybsze znalezienie ścieżki:
Przetestuj różne warianty np. „dy”, „dx”, „5*dx”
Zanotuj najlepszy rezultat.
Dlaczego algorytm tak wolno porusza się wewnątrz labiryntu?
W celu lepszego zrozumienia zachowania algorytmu włącz pokazywanie wartości (kliknij „Show values”):
f - oszacowania długości trasy.
g - długości dotychczasowej ścieżki.
h - oszacowania od punktu docelowego (heurystyki).
Uruchom wyszukiwanie dwukierunkowe w we wszystkich algorytmach (zaznacz opcje „Bi-directional”).
Przetestuj różne heurystyki.
Czy Twoja najlepsza heurystyka w wyszukiwaniu jednokierunkowym jest w którymś przypadku lepsza?
Dla tego konkretnego przypadku zaproponuj najszybszy sposób wyznaczania najkrótszej ścieżki pomiędzy punktami końcowymi z wykorzystaniem przeszukiwania jednokierunkowego.
Spróbuj osiągnąć czas poniżej 50ms i poniżej 200 operacji

Jak tego dokonać

5 Problem n-puzzli
 Opisane w poprzednich sekcjach algorytmy nie są ograniczone jedynie do dziedziny planowania tras przejazdu. W ogólnym przypadku pozwalają na znajdywania najkrótszych ścieżek w dowolnych¹ grafach, które dzięki abstrakcyjnej strukturze mogą modelować wiele problemów, będących obiektami zainteresowania sztucznej inteligencji. Sztandarowym przykładem może być tutaj problem n-puzzli, czyli popularna zagadka-układanka, w której należy odtworzyć zadany wzorzec poprzez przesuwanie puzzli zamkniętych w kwadratowej ramce. Jeżeli ktoś nigdy nie grał, to może spróbować na tej stronie lub w przypadku braku wtyczki Flash tutaj.
Opisane w poprzednich sekcjach algorytmy nie są ograniczone jedynie do dziedziny planowania tras przejazdu. W ogólnym przypadku pozwalają na znajdywania najkrótszych ścieżek w dowolnych¹ grafach, które dzięki abstrakcyjnej strukturze mogą modelować wiele problemów, będących obiektami zainteresowania sztucznej inteligencji. Sztandarowym przykładem może być tutaj problem n-puzzli, czyli popularna zagadka-układanka, w której należy odtworzyć zadany wzorzec poprzez przesuwanie puzzli zamkniętych w kwadratowej ramce. Jeżeli ktoś nigdy nie grał, to może spróbować na tej stronie lub w przypadku braku wtyczki Flash tutaj.
Z punktu widzenia informatyki rozwiązaniem problemu n-puzzli jest skończony ciąg ruchów [m_1, m_2, …, m_k], których wykonanie w danej kolejności pozwoliłoby na przejście z zadanego stanu początkowego S do stanu końcowego G.
¹oczywiście, istnieją pewne ograniczenia, np. nie może istnieć w grafie cykl o ujemnej sumie wag należących do niego krawędzi. W takim wypadku dla pewnych wierzchołków najkrótsza ścieżka nie istnieje. W problemie znajdywania najkrótszej trasy na mapie sytuacja taka w oczywisty sposób nie występuje.
Reprezentacja grafowa
Problem n-puzzli w prosty sposób daje się przedstawić w postaci problemu znajdowania najkrótszej ścieżki w nieskierowanym grafie:
Za wierzchołki grafu należy przyjąć wszystkie możliwe kombinacje puzzli na planszy.
Między wierzchołkami grafu v_1 i v_2 istnieje krawędź wtedy i tylko wtedy, gdy istnieje pojedynczy ruch, który pozwala na przejście między tymi stanami.
Przy takim kodowaniu problemu, do jego rozwiązania może zostać użyty dowolny z algorytmów zaprezentowanych w poprzednich zadaniach.
Zadania
Oszacuj liczbę wierzchołków w grafie reprezentującym puzzle 5×5. Następnie odpowiedz na poniższe pytania:
Czy taki graf zmieści się w pamięci współczesnego komputera (załóż, że jeden wierzchołek zajmuje w pamięci 32 bity, zignoruj krawędzie)?
Czy graf musi być w całości wygenerowany przed przystąpieniem do szukania rozwiązania?
-
Przeczytaj opis problemu i instrukcję obsługi.
Użyj narzędzia w trybie „single-step” na domyślnych stanach początkowych i końcowych.
Wypróbuj różne algorytmy i heurystyki, zapisz liczbę odwiedzonych przez nie wierzchołków.
Czym różni się heurystyka „Tiles Out-of-place” od heurystyki „Manhattan Distance”? Możesz spróbować zaobserwować różnice na inaczej zdefiniowanych stanach początkowych/końcowych.
-
6 Świat klocków
 Kolejnym problemem, który może zostać zamodelowany przy użyciu grafu jest, tzw. świat klocków. Problem jest pozornie mało ambitny: polega na znalezieniu odpowiedniej sekwencji ruchów, pozwalających na przestawienie klocków ze stanu początkowego do zadanego stanu końcowego. W świecie klocków istnieje określona liczba klocków (tradycyjnie każdy klocek wyróżnia narysowana na nim literka) oraz kilka kolumn, w których te klocki mogą leżeć. Każdy klocek leży na dnie jednej z kolumn lub umieszczony jest na innym klocku. Przykładowe stany początkowy i końcowy pokazane są na obrazu powyżej. Jedyną możliwą akcją w świecie klocka jest podniesienie klocka, który jest na szczycie kolumny i położenie go na szczycie kolumnie.
Kolejnym problemem, który może zostać zamodelowany przy użyciu grafu jest, tzw. świat klocków. Problem jest pozornie mało ambitny: polega na znalezieniu odpowiedniej sekwencji ruchów, pozwalających na przestawienie klocków ze stanu początkowego do zadanego stanu końcowego. W świecie klocków istnieje określona liczba klocków (tradycyjnie każdy klocek wyróżnia narysowana na nim literka) oraz kilka kolumn, w których te klocki mogą leżeć. Każdy klocek leży na dnie jednej z kolumn lub umieszczony jest na innym klocku. Przykładowe stany początkowy i końcowy pokazane są na obrazu powyżej. Jedyną możliwą akcją w świecie klocka jest podniesienie klocka, który jest na szczycie kolumny i położenie go na szczycie kolumnie.
Kodowanie problemu w postaci nieskierowanego grafu działa podobnie jak w n-puzzlach: każdy wierzchołek to możliwe ustawienie klocków; każda krawędź między wierzchołkami v_1 i v_2 odpowiada dozwolonemu przełożeniu klocka, które stan v_1 przekształca w stan v_2 (i vice versa).
Heurystyka
Chociaż świat klocków wydaje się być dziecinny, nie funkcjonują w nim standardowe heurystyki napotkane w poprzednich sekcjach, podczas, gdy jego najtrudniejsze wersje są NP-zupełne. Przykładowa heurystyka dla problemu klocków może zostać zdefiniowana w dwóch następujących regułach:
Jeżeli klocek leży nie w tej kolumnie, w której powinien (w stanie docelowym), należy dodać 1 do wartości heurystyki — intuicyjnie: z pewnością konieczne będzie chociaż jedno przełożenie tego klocka
Jeżeli klocek leży w dobrej kolumnie, ale struktura klocków pod nim nie zgadza się ze stanem docelowym, należy dodać 2 do heurystyki — intuicyjnie: z pewnością trzeba będzie ten klocek przełożyć na inną kolumnę, by potem go przełożyć z powrotem na dobrą kolumnę.
Te dwie reguły są sprawdzane i wykonywane dla każdego klocka osobno.
Zadania
-
Uruchom rozpakowany applet (narzędzie jest proste, w razie czego tu jest
instrukcja obsługi)
Aby uruchomić wpisz w konsoli javaws search.jnlp
Jeżeli program nie chce się uruchomić ze względu na poziom bezpieczeństwa, dodaj aispace do listy wyjątków: uruchom w konsoli ControlPanel → zakładka Security → Edit Site List… → Dodaj wpis http://www.aispace.org/ → zatwierdź
Otwórz w narzędziu załączony graf blocks.xml.
Dokończ budowę grafu:
Dodaj wierzchołki dla pozostałych stanów świata klocków:
Podpowiedź: Etykieta węzła opisuje stan 3-kolumnowego, 2-klockowego świata, np. „|ab| | |” oznacza, że w pierwszej kolumnie klocek „a” leży na klocku „b”, a pozostałe kolumny są puste.
W każdym wierzchołku wpisz ręcznie wartość heurystyki wyliczonej według dwóch reguł podanych powyżej (dla stanu początkowego została już policzona).
Dodaj krawędzie między odpowiednimi stanami.
Uruchom na gotowym grafie algorytm przeszukiwania i zapisz wyniki.
7 Zagadnienie automatycznego planowania
Podczas tego laboratorium dotknęliśmy bardzo ważnej i wszechobecnej (przemysł, robotyka, gry komputerowe, etc.) dziedziny AI, jaką jest planowanie. Zasadniczo planowanie polega na znalezieniu ciągu akcji (zwanego planem), który po zastosowaniu na stanie początkowym S, doprowadzi do osiągnięcia stanu docelowego G. Każda akcja posiada warunki, w których może zostać wykonana oraz skutki jej zastosowania. Planowanie jest trudne, o ile nie założy się odpowiednich ograniczeń na akcje, jego złożoność jest klasy PSPACE-zupełnej. Trzeba ponadto zauważyć, że w realnych niezabawkowych problemach występują dodatkowe czynniki zwiększające trudność problemu:
niepełna wiedza o aktualnym stanie (np. brak odpowiednich sensorów w robocie)
niepewność wynikająca z zawodności akcji (niektóre akcje mogą się zwyczajnie nie powieść)
wykonywanie akcji zajmuje czas — plan powinien brać pod uwagę temporalny wymiar problemu
mogą wydarzać się zdarzenia niezależne od agenta — np. wypadek drogowy na drodze autonomicznego samochodu.
Świat bloków jest jednym z najbardziej popularnych problemów/zabawek w świecie planowania.
STRIPS
Jednym z najbardziej znanych programów planujących jest powstały na Stanfordzie w latach 70 program STRIPS. Używana w nim reprezentacja wiedzy jest do dzisiaj podstawą większości narzędzi planujących. Przykładowa struktura problemu może być zdefiniowana następująca:
Mając taką reprezentację wiedzy, klasyczny program planujący działa według bardzo prostego wzorca (dla zadanego stanu końcowego G i początkowego S):
Sprawdź, czy aktualny stan jest stanem końcowym. Jeżeli tak, wypisz znaleziony plan.
Znajdź fakt F, który jest prawdziwy w stanie końcowym, ale nie jest prawdziwy aktualnym stanie.
Znajdź akcję A, którą na liście faktów dodawanych F.
Uruchom rekurencyjnie rutynę planującą, aby znaleźć plan doprowadzający do stanu, który spełnia warunki wykonania akcji A.
Wykonaj akcję A i zaktualizuj aktualny stan do stanu S'.
Uruchom rutynę planującą zaczynając od nowego stanu S'.
Efektem powyższej procedury będzie „odwrócony plan”, aby miał sens, należy go wypisać idąc od końca. Drugi haczyk polega na unikaniu zapętlenia w planowaniu - jeżeli chcemy osiągnąć warunki wykonania akcji A (punt 4.) należy wyłączyć ją z procesu planowania.
Pod poniższym linkiem znajduje się prosta(cka) implementacja solvera STRIPS w języku Prolog.
Zadania
Należy pobrać uzupełnić powyższy program w Prologu o informacje potrzebne do rozwiązania problemu bloków (sekcje %TODO:). Objaśnienia:
dla wygody planowania możemy pominąć numery kolumn, a stan może być reprezentowane przez pięć typów faktów (przykładowe stany można zobaczyć w sekcji EXAMPLES OF USAGE):
ontable/1 — dany klocek leży na stole, np. ontable(a)
on/2 — dany klocek leży na drugim klocku, np. on(a,b)
clear/1 — na danym klocku nic nie leży, np. clear(a)
holding/1 — dany klocek został właśnie podniesiony, np. holding(a)
handempty/0 — żaden klocek nie jest aktualnie podniesiony, czyli: handempty
potrzebne są cztery rodzaje akcji (jedna z nich już jest zaimplementowana)
połóż klocek X na klocku Y: wykonalna, o ile klocek X jest aktualnie trzymany, a Y jest czysty. Po wykonaniu akcji klocek X leży na klocku Y i jest czysty, klocek Y przestaje być czysty i żaden klocek nie jest aktualnie podniesiony.
zdejmij klocek X z klocka Y: wykonalna, o ile klocek X jest czysty i aktualnie leży na klocku Y. Po wykonaniu akcji klocek X przestaje być czysty, przestaje leżeć na klocku Y i zostaje podniesiony. Klocek Y natomiast staje się czysty.
połóż klocek X na stole: analogicznie do akcji pierwszej z taką różnicą, że nie ma wymagań i zmian względem Y
zdejmij klocek X ze stołu: analogicznie do akcji drugiej
Proszę uruchomić planowanie dla trzech załączonych przykładów oraz dla jednej zamodelowanego samodzielnie.
Proszę usunąć z części warunkowej akcji wszystkie warunki o postaci clear/1 i ponownie uruchomić planowanie dla czterech przypadków.
jaką wartość mają tak wygenerowane plany?
-





