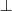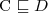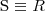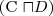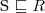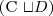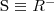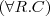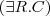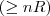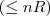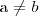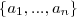Description Logics and OWL in the Semantic Web
Outline
Semantic Web
a vision of the Semantic Web first proposed in May 2001 in an
article by
Tim Berners-Lee,
James Hendler and
Ora Lassila published by Scientific American as
“an extension of the current one, in which information is given well-defined meaning, better enabling computers and people to work in cooperation.”
“If HTML and the Web made all the online documents look like one huge book, RDF, schema, and inference languages will make all the data in the world look like one huge database” - Tim Berners-Lee, Weaving the Web, 1999
the idea was to make the Web content “understandable” for machines and enable automated reasoning over it
the goal was to create an environment where software agents could solve complex searching and reasoning tasks
the way to do it is to present information in some standarized formats (markup languages) and give the means to reason about it
-
Semantic Web Layer Cake(s)
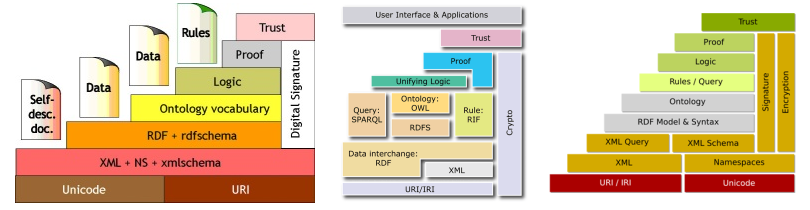
web content encoded in
Unicode, resources identified by
URI the structure provided by →
XML tags
metadata (basic/primitive semantics) encoded in →
RDF semantics (meaning and relations between concepts) given by means of →
Ontologies:
OWL, (somehow also
RDFS)
-
Resource Description Framework
RDF is a framework for describing resources on the web
written in XML and designed to be read by computers
uses Web identifiers (URIs) to identify resources (documents, pictures, paragraphs, books, …)
describes resources with properties and property values
RDF Statements are <subject, predicate, object> triples
a graphical formalism for representing metadata
-
RDF Schema
RDFS - difficulties
Desirable features identified for Web Ontology Language
Extends existing Web standards such as XML, RDF, RDFS
Easy to understand and use
Should be based on familiar KR idioms
Formally specified
Of “adequate” expressive power
Possible to provide automated reasoning support
Towards Web Ontology Language...
Two languages were developed to satisfy above requirements
OIL: developed by group of (largely) European researchers (several from EU OntoKnowledge project)
DAML: developed by group of (largely) US researchers (in
DARPA DAML programme)
-
Development was carried out by “Joint EU/US Committee on Agent Markup Languages”
DAML+OIL submitted to
W3C as basis for standardisation
OWL language now a W3C Recommendation
OWL is based on Description Logics
Ontology in Computer Science
Description Logics
Description Logics
DL are a family of Knowledge Representation formalisms
they describe world of interest by means of concepts and relations between them
they provide formal semantics and inference services
Description Logics are a family of knowledge representation formalisms.
Their underlying idea is to represent the world of interest in terms of concepts, individuals and relations between them.
Description Logics are related to semantic networks and frame systems.
Contrary to them, thanks to their connection to First Order Logic, they provide a formal semantics and inference services.
History and Background
Examples of DL expressions
KR system based on DL
A Knowledge Representation System based on DL provides means to set up a knowledge base, to manipulate it and reason about it
The knowledge base consists of
TBox - terminology, intensional representation
ABox - assertions about individuals, extensional representation

Relation to First Order Logic
-
concept names ⇔ unary predicates
atomic roles ⇔ binarty predicates
concepts ⇔ formulae with one free variable
DL and FOPL Compared
Applications of DL and DL-based systems
Software Engineering
1 of the first: CLASSIC - Software Information System Configuration
Medicine (decision support, ontologies)
Natural Language processing
Database management
Creating ontologies for Semantic Web
Basic DL
elementary descriptions are atomic concepts and atomic roles
complex descriptions built from them inductively with concept constructors
Description Languages are distinguished by the constructors they provide
AL (Attributive Language) - is a minimal language of practical interest
AL syntax
Symbols
construction syntax rule:
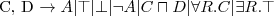
-
AL semantics
AL syntax and semantics table
Examples
atomic concepts:
Person,
Female,
Elephant note: without stating it explicitly there is no relation between Person, Female and Elephant, they just denote some sets
a female person:

a female elephant:
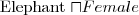
a not-female person:
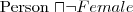
atomic role: hasChild
a person with children
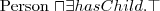
a person all of whose children are female
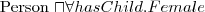
a person without children
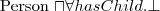
DL "families"
resulting languages:
![LaTeX \mathcal{AL} [ \mathcal{U}][ \mathcal{E} ][\mathcal{N} ][\mathcal{C} ]](/lib/exe/fetch.php?media=wiki:latex:/img99b799b4d5ddcd9782d4ebfc1036c87e.png)
ALC
Smallest
propositionally closed (propositionally closed languages provide, either implicitly or explicitly, conjunction, union and negation of class descriptions DL is
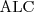
equivalence with
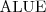
:
Concepts constructed using booleans:
restricted quantifiers:
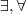
Only atomic roles
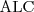
corresponds to a fragment of FOL obtained by restricting the syntax to formulas containing only 2 variables
Terminologies (TBox)
terminologies may be
cyclic or acyclic acyclic terminologies have definitiorial impact. Their semantics is called descriptive semantics. Cyclic terminologies (used e.g. to model recursive structures ) needs fixed point semantics… (see F.Baader,W.Nutt - Basic Description Logics in DL Handbook.) terminologies may include
specialization statements - axioms of the form
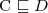
Selected definitions...
Name symbols - symbols that occur on the left-hand side of axioms
Base symbols - symbols that occur ONLY on the right-hand side of axioms
Base interpretations - interpretation that interprets only base symbols
Extension - interpretation that interpret also the name symbols and
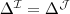
Terminology is definitorial if every base interpretation has exactly one extension that is a model of T.
TBox semantics
an interpretation (function)
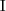
maps each concept name to a subset of the domain
an interpretation satisfies an axiom
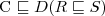
if:
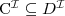
or
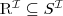
an interpretation
I satisfies a concept definition
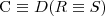
if:

or
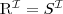
TBox Example
World Description (ABox)
an ABox contains extensional knowledge about the domain of interest (individuals)
concept assertions, e.g. C(a)
role assertions, R(b,c)
ABox semantics
ABox Example
Nominals in TBox
DL Inference
Reasoning tasks
Open World Assuption
Rules
Reasoning algorithms
Reasoning tasks for TBox
satisfiability
a concept C is satisfiable with respect to T if there exists a model (an interpretation) I of T such that
is not empty
subsumption
a concept C is subsumed by a concept D w.r.t. T if
for every model I of T
equivalence
two concepts C and D are equivalent w.r.t. T if

for every model I of T
disjointness
two concepts C and D are disjoint w.r.t. T if
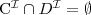
for every model I of T
Reasoning tasks for ABox
Reduction of reasoning tasks
Open World semantics
DL Knowledge Base vs. Relational Database
database schema ↔ TBox
instance with data ↔ ABox
contrary to relational databases, absence of information in ABox means lack of knowledge, not a negative information
ABox represents possibly infinitely many interpretations
open-world semantics requires nontrivial reasoning, answering queries is more complex
Rules
in some DL systems in addition to TBox and ABox one can use trigger rules to express knowledge
C ⇒ D
if an individual is proved to be an instance of C, then derive that it is also an instance of D
C ⇒ D is not a logical implication, it does not mean that ¬D → ¬C

Structural subsumption algorithms
Tableau algorithms
use of the fact that: C is subsumed by D ⇔
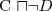
is unsatisfiable
start from ground facts (ABox axioms)
syntactic decomposition using tableaux expansion rules
Tableau rules correspond to constructors in logic (
)
Some rules are nondeterministic (e.g.,
) (In practice, this means search)
Inferring constraints on (elements of) model
Stop when no more rules applicable or clash occurs
Inference Example
We know that:
We can infer that:
We know that:
We can infer that:
-
-
Language extensions
DL family vs. reasoning complexity
OWL - Web Ontology Language
OWL
DL and OWL
OWL exploits results of 15+ years of DL research
Well defined (model theoretic) semantics
Formal properties well understood (complexity, decidability)
Known reasoning algorithms
Implemented systems (highly optimised)
OWL ontology equivalent to DL KB (Tbox + Abox)
OWL DL based equivalent to SHOIN(D) DL
3 species of OWL
OWL Full is union of OWL syntax and RDF
OWL DL is restricted to FOL fragment (≈ DAML+OIL)
OWL Lite is “simpler” subset of OWL DL
Equivalent to
SHIF(D) role transitivity(S) + role hierarchy (H) + inverse (I) + functionality (F) + datatype properties, data values or data types (D)= SHIF(D)
OWL and DL Syntax Compared
OWL - Abstract syntax
Ontology(
Class(pp:male partial)
Class(pp:adult partial)
Class(pp:elderly partial pp:adult)
Class(pp:pet complete restriction(pp:is_pet_of someValuesFrom(owl:Thing)))
Class(pp:animal partial restriction(pp:eats someValuesFrom(owl:Thing)))
/* Vegetarians do not eat animals or parts of animals */
Class(pp:vegetarian complete
intersectionOf(pp:animal
restriction(pp:eats allValuesFrom(complementOf(pp:animal)))
restriction(pp:eats
allValuesFrom(complementOf(restriction(pp:part_of
someValuesFrom(pp:animal)))))))
DisjointClasses(pp:dog pp:cat)
ObjectProperty(pp:eaten_by)
ObjectProperty(pp:eats inverseOf(pp:eaten_by) domain(pp:animal))
SubPropertyOf(pp:has_pet pp:likes)
Individual(pp:Tom type(owl:Thing))
Individual(pp:Tibbs type(pp:cat))
OWL - XML syntax
<owl:Class>
<owl:intersectionOf rdf:parseType="collection">
<owl:Class rdf:about="#Person"/>
<owl:Restriction>
<owl:onProperty rdf:resource="#hasChild"/>
<owl:toClass>
<owl:unionOf rdf:parseType="collection">
<owl:Class rdf:about="#Doctor"/>
<owl:Restriction>
<owl:onProperty rdf:resource="#hasChild"/>
<owl:hasClass rdf:resource="#Doctor"/>
</owl:Restriction>
</owl:unionOf>
</owl:toClass>
</owl:Restriction>
</owl:intersectionOf>
</owl:Class>
Increased Expressive Power - Datatypes and Nominals
Reasoning in OWL DL
Future challenges
Rule languages over OWL
If you want to know more
-
-
-
Protege - a tool for creating/editing ontologies
-
-
References
Thank you


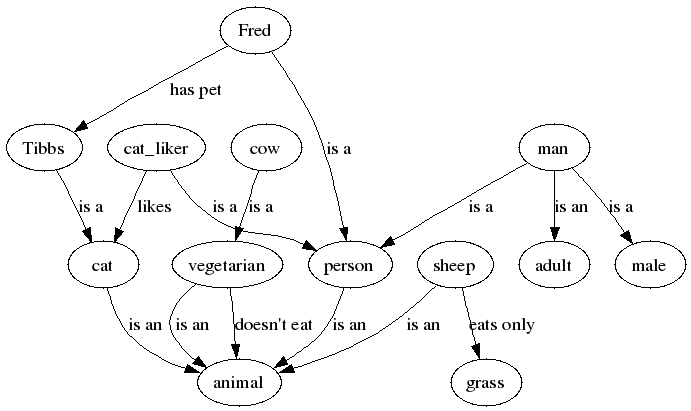
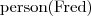 - Fred is a person
- Fred is a person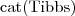 Tibbs is a cat
Tibbs is a cat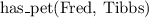 - Fred has a pet which is Tibbs
- Fred has a pet which is Tibbs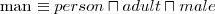 - A man is an adult male person
- A man is an adult male person 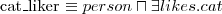 - A cat liker is a person and there exists a cat that he/she likes
- A cat liker is a person and there exists a cat that he/she likes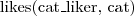 - (every) cat liker likes a cat
- (every) cat liker likes a cat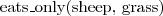 - (every) sheep eats only grass
- (every) sheep eats only grass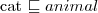 a cat is an animal (hierarchy of concepts)
a cat is an animal (hierarchy of concepts)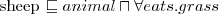 a sheep is an animal which eats only grass (it's a necessary but not sufficient condition)
a sheep is an animal which eats only grass (it's a necessary but not sufficient condition)






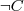
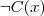
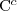 (complement of set)
(complement of set)
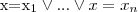

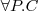
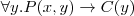
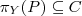
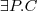
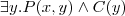
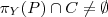 (Π - projection)
(Π - projection)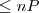
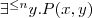
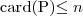 (card - cardinality)
(card - cardinality)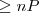
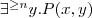
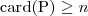

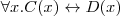
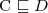
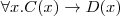
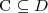
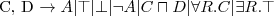
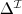 - a non-empty set to which all the symbols and relations are mapped
- a non-empty set to which all the symbols and relations are mapped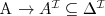
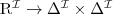
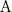
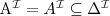
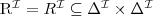

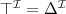
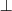
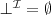
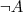
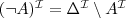
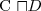
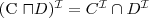
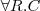
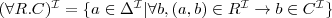
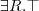
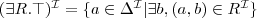

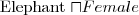
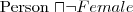
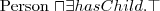
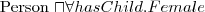
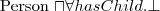
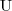 - union :
- union : 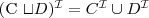
 - full existential quantification :
- full existential quantification : 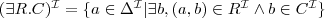
 - number restrictions:
- number restrictions: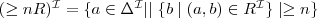
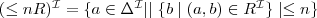
 - negation :
- negation : 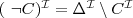
![LaTeX \mathcal{AL} [ \mathcal{U}][ \mathcal{E} ][\mathcal{N} ][\mathcal{C} ]](/lib/exe/fetch.php?media=wiki:latex:/img99b799b4d5ddcd9782d4ebfc1036c87e.png)
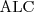
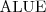 :
: 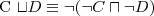
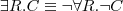
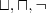
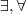
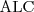 corresponds to a fragment of FOL obtained by restricting the syntax to formulas containing only 2 variables
corresponds to a fragment of FOL obtained by restricting the syntax to formulas containing only 2 variables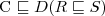 or
or 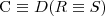
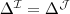
 maps each concept name to a subset of the domain
maps each concept name to a subset of the domain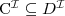 or
or 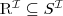
 or
or 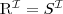
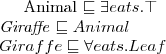
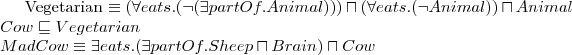
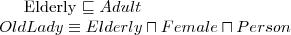
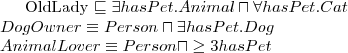
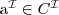
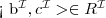

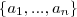
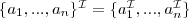
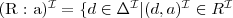
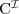 is not empty
is not empty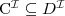 for every model I of T
for every model I of T for every model I of T
for every model I of T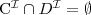 for every model I of T
for every model I of T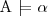 iff every interpretation I which satisfies A also satisfies α
iff every interpretation I which satisfies A also satisfies α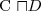 is subsumed by ⊥
is subsumed by ⊥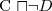 is unsatisfiable (this is used in tableau-based algorithms)
is unsatisfiable (this is used in tableau-based algorithms)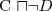 is unsatisfiable
is unsatisfiable )
)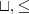 ) (In practice, this means search)
) (In practice, this means search)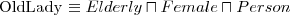


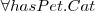
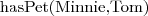 ,
,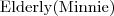 ,
,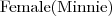
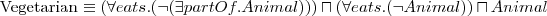
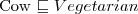
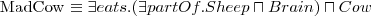
 for functional number restrictions (e.g., ≤1hasMother)
for functional number restrictions (e.g., ≤1hasMother) for qualified number restrictions (graded modalities, e.g., ≥2hasChild.Doctor))
for qualified number restrictions (graded modalities, e.g., ≥2hasChild.Doctor)) for nominals/singleton classes (e.g., {Italy})
for nominals/singleton classes (e.g., {Italy})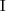 for inverse roles (e.g.,
for inverse roles (e.g.,  )
)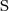 Role transitivity - often used for
Role transitivity - often used for  extended with transitive roles
extended with transitive roles Role hierarchy (e.g.,
Role hierarchy (e.g., 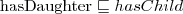 )
)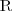 Complex role inclusions: RoS ⊆ R, RoS ⊆ S
Complex role inclusions: RoS ⊆ R, RoS ⊆ S Use of datatype properties, data values or data types
Use of datatype properties, data values or data types