Laboratorium 1 - Wprowadzenie do GNU Octave
Środowisko Octave jest wolnym odpowiednikiem pakietu MATLAB.
Dokumentacja
Instalacja i uruchamianie
W przypadku większości systemów Linux, pakiet Octave można zainstalować bezpośrednio z repozytorium:
$ sudo apt-get install octave
W przypadku systemu Windows i OS X, oprogramowanie Octave można ściągnąć ze strony projektu: GNU Octave.
W systemie Linux uruchamiamy środowisko za pomocą polecenia
$ octave
W konsoli Octave możemy wykonywać wszystkie podstawowe polecenia umożliwiające nawigację w systemie plików (cd, ls, etc).
Składnia
Typy i zmienne
W języku Octave, nie prototypujemy zmiennych. Typy określane są automatycznie, tak jak w PHP, czy Bashu.
zmienna = 'moja zmienna';
zmienna = 12.34;
zmienna = [2 3 4; 3 4 5];
Jednym z podstawowych typów danych w Octave są wektory i macierze.
Definiujemy je za pomocą nawiasów kwadratowych.
Wartości w wierszach oddzielamy spacjami lub przecinkami.
Wiersze oddzielamy znakiem średnika.
Załóżmy że chcemy zdefiniować następującą macierz i przypisać ją do zmiennej M:
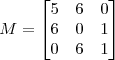
W Octave zapiszemy ją jako:
M = [5 6 0; 6 0 1; 0 6 1]
Aby odwołać się do danego elementu macierzy, lub wektora używamy nawiasów okrągłych.
Uwaga  W Octave indeksowanie rozpoczyna się od 1 a nie jak w popularnych językach programowania od 0! Np. Aby pobrać/przypisać wartość elementu z pierwszego wiersza i drugiej kolumny macierzy M, piszemy:
W Octave indeksowanie rozpoczyna się od 1 a nie jak w popularnych językach programowania od 0! Np. Aby pobrać/przypisać wartość elementu z pierwszego wiersza i drugiej kolumny macierzy M, piszemy:
M(1,2)=7
Jako wynik otrzymujemy:
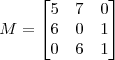
Octave umozliwia równiez odwoływanie się do całych kolumn i wierszy w danej macierzy:
M(:,3) % zwróci [0;1;1]
M(2,:) % zwróci [6 0 1]
Sprawdź co jak zadziała poniższy kod:
M = [5 6 0; 6 0 1; 0 6 1];
M([2 3],[1 2])
Zakresy
Zakresy tworzy się za pomocą znaku dwukropka. Służą one do definiowania prostych zestawów danych, a także do odwoływania się do danych w wektorach i macierzach.
Przetestuj działanie poniższych poleceń
zeros(1,10)
zeros(2,10)
ones(1,10)
range = [1:10]
range = [1:0.3:10]
range(5:10)
Operatory arytmetyczne
Octave udostępnia podstawowe operatory arytmetyczne zarówno dla macierzy jak i skalarów. Pełny zbiór operatorów dostępny jest w dokumentacji Octave.
Uwaga  Zwróć uwagę na działanie operatorów połączonych z kropką!
Zwróć uwagę na działanie operatorów połączonych z kropką!
Przetestuj działanie poniższego kodu.
A = [0.5 0.5; 1 1];
B = [2 2; 2 2];
A * B
A .* B
B ^ 2
B .^ D
Instrukcje sterujące
Octave udostępnia powszechnie znane z innych języków programowania instrukcje sterujące. Pełny opis instrukcji sterujących można znaleźć w dokumentacji Octave
Definiowanie funkcji
Szczegółowe dane na temat definiowania funkcji można znaleźć w dokumentacji Octave. Poniżej kilka podstawowych infromacji:
Funkcje najczęściej definiujemy w osobnych plikach z rozszerzeniem .m
Nazwa funkcji musi zgadzać się z nazwą pliku!
Wywoływanie funkcji odbywa się poprzez podanie jej nazwy i listy argumentów.
Podczas wywoływania funkcji musimy znajdować się w katalogu w którym dana funkcja jest zapisana.
W Octave nie zwracamy wartości za pomocą return. Po prostu przypisujemy ją do zmiennej podanej jako element zwracany
Komentarze w kodzie wstawiamy za pomocą %
Przykładowa definicja funkcji:
- srednia.m
function W = srednia(dane)
% funkcja obliczająca średnią elementów w wektorze
W = sum(dane)/length(dane);
end
Aby wywołać funkcje z przykładu powyżej wykonujemy polecenie:
Wynik = srednia([2 3 4 5 6 7 8]);
Jeśli funkcja ma zwracać więcej niż jeden argument, zapisujemy to w ten sposób:
- myFind.m
function [IndexX,IndexY] = myFind(M,V)
% Funkcja poszukująca wartości V w macierzy M
% Funkcja zwraca indeksy znalezionej wartości, lub -1,-1
[rows,cols] = size(M);
IndexX = IndexY =-1;
for i=1:rows,
for j=1:cols
if M(i,j) == V
IndexX = i;
IndexY = j;
return;
endif
end
end
end
Aby pobrać wartości zwracane przez funkcję powyżej wpisujemy np.:
[X,Y] = myFind(M,6);
Rysowanie wykresów
Do rysowania wykresów używamy funkcji:
plot - rysowanie wykresów 2D
plot3d - rysowanie wykresów 3D
mesh - rysowanie płaszczyzn
Porównaj działanie funkcji na poniższych przykładach. Jaka jest różnica pomiędzy plot3 a mesh?
Plot2
x = [0:0.01:10];
y = sin(x);
plot(x,y);
Plot3
t = 0:0.1:10*pi;
r = linspace (0, 1, numel (t));
z = linspace (0, 1, numel (t));
plot3 (r.*sin(t), r.*cos(t), z);
Mesh
tx = ty = linspace (-8, 8, 41)';
[xx, yy] = meshgrid (tx, ty);
r = sqrt (xx .^ 2 + yy .^ 2) + eps;
tz = sin (r) ./ r;
mesh (tx, ty, tz);
Dobre praktyki
Jeśli tylko jest to możliwe, używaj funkcji wbudowanych. Na przykład zamiast pisać swoją własną funkcję srednia lepiej było wykorzystać wbudowaną funkcję mean.
Jeśli to tylko możliwe, staraj się wykorzystywać operacje na macierzach, zamiast pętli.
Zawsze definiuj wcześniej wektor/macierz z która pracujesz (chyba że jest ona bezpośrednim wynikiem jakichś operacji). Np.:
M = zeros(3,3);
[x,y] = size(M);
for i=1:x
for j=1:y
M(i,j) = rand;
end
end
Ćwiczenia
Operacje podstawowe I
Zakładając, że mamy następującą macierz

Jakie indeksowanie macierzy A pozwoli na wyciągnięcie z niej następującej macierzy:
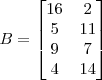
Operacje podstawowe II
Napisz funkcję znajdującą najmniejszy i największy element w macierzy i zwracającą te wartości.
Podpowiedź użyj zbudowanych funkcji min i max.
Wartość wektora
Napisz funkcje wyznaczającą długość (normę) wektora podanego jako parametr, która określona jest wzorem:
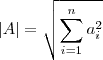
Odchylenie standardowe I
Napisz funkcję wyznaczającą odchylenie standardowe dla wartości wektora podanego jako parametr. Odchylenie standardowe dane jest wzorem:
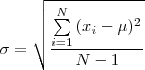
Gdzie 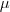 to średnia, a N to liczba wszystkich elementów w probie.
to średnia, a N to liczba wszystkich elementów w probie.
Odchylenie standardowe II
Przyjmij, że tym razem parametrem funkcji nie jest wektor, ale macierz. Funkcja powinna obliczyć odchylenia standardowe dla każdego wiersza macierzy osobno i zwrócić wektor odchylen standardowych.
Uwaga Pamiętaj o zadaniu Operacje Podstawowe I i II!
Wydajność I
Dla funkcji napisanych w poprzednich dwóch zadaniach (Długość wektora oraz Odchylenie Standardowe I) dopisz ich odpowiedniki wektorowe (lub z użyciem pętli) i przetestuj ich działanie na wygenerowanym losowo zbiorze 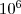 liczb.
liczb.
Aby wygenerować dane użyj:
data = rand(1,10^6);
Porównaj czasy wykonywania funkcji:
timestart = time();
%Wywolanie funkcji
timestop = time();
printf('Czas wykonania to %d sekund.\n',(timestop-timestart));
Jak zmienią się czasy gdy zmienimy ilość danych z 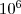 na
na 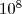 ?
O ile wolniej (procentowo) wykonuje się algorytm wyznaczający odchylenie standardowe wykorzystujący wbudowaną funkcję obliczającą średnią od tego, który wykorzystuje funkcję srednia napisaną przez nas?
?
O ile wolniej (procentowo) wykonuje się algorytm wyznaczający odchylenie standardowe wykorzystujący wbudowaną funkcję obliczającą średnią od tego, który wykorzystuje funkcję srednia napisaną przez nas?
Wydajność II
Jak poprawic wydajnośc następujących fragmentów kodu:
Przykład I
A = zeros(10,10)
v = zeros(10, 1);
x = zeros(10, 1);
for i = 1:10
for j = 1:10
x(i) = v(i) + A(i, j) * v(j);
end
end
Przykład II
for i = 1:7
for j = 1:7
A(i, j) = log (X(i, j));
B(i, j) = X(i, j) ^ 2;
C(i, j) = X(i, j) + 1;
D(i, j) = X(i, j) / 4;
end
end
Rysowanie wykresu funkcji
Napisz funkcję która będzie wyznaczała wartości funkcji z obrazka poniżej. Wyrysuj wartości tej funkcji na wykresie w przedziale od -10 do 10 z krokiem 0.5.
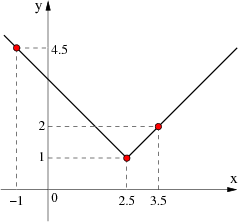
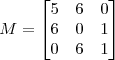
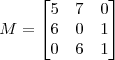

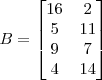
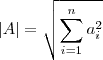
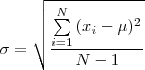
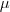 to średnia, a N to liczba wszystkich elementów w probie.
to średnia, a N to liczba wszystkich elementów w probie.
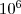 liczb.
liczb.
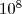 ?
O ile wolniej (procentowo) wykonuje się algorytm wyznaczający odchylenie standardowe wykorzystujący wbudowaną funkcję obliczającą średnią od tego, który wykorzystuje funkcję srednia napisaną przez nas?
?
O ile wolniej (procentowo) wykonuje się algorytm wyznaczający odchylenie standardowe wykorzystujący wbudowaną funkcję obliczającą średnią od tego, który wykorzystuje funkcję srednia napisaną przez nas?
