To jest stara wersja strony!
Opis
Joanna Jaworek, jaworek.joanna@gmail.com
Temat: Programowanie z wykorzystaniem ograniczeń CLP. Sekwencjonowanie DNA- projekt z wykorzystaniem biblioteki JPL swi-prolog.
Wstęp
Niniejsza praca składa się z sześciu rozdziałów: programowanie logiczne, programowanie logiczne z ograniczeniami, CHR, problemy NP-trudne, sekwencjonowanie DNA oraz podsumowanie. Celem pierwszych dwóch rozdziałów jest przedstawienie koncepcji programowania w prologu oraz zaprezentowanie kilku zaimplementowanych przykładów. Rozdział trzeci przedstawia ciekawe wykorzystanie programowania CLP/CHR do rozwiązywania problemów NP-trudnych, czyli o dużej złożoności czasowej. Tutaj także zaprezentuję aplikację umożliwiającą testowanie programów. Rozdział czwarty odwołuje się do ostatnich nowinek ze świata nauki, które pokładają dużą nadzieję w sekwencjonowanie DNA właśnie w prologu. Rozdział ten także zawiera moją własną implementację prostego sekwencjonowanie DNA. Ostatni rozdział to podsumowanie referatu oraz przedstawienie innych implementacji platform oraz narzędzi opartych na CLP.
Programowanie logiczne
Teoria
Programowanie logiczne narodziło się na początku lat 70-tych jako rezultat wcześniejszych prac w zakresie automatycznego dowodzenia twierdzeń i sztucznej inteligencji. Jednak dopiero w chwili opracowania języka PROLOG nabrało walorów praktycznej użyteczności. Metoda programowania w języku logiki stała się podstawą opracowanie języka maszynowego oraz języka programowania wiedzy. Podstawową cechą odróżniającą programowanie logiczne od konwencjonalnych technik programowania jest reprezentowanie wiedzy w sposób jawny, niezwiązany ze sposobem jej użycia w celu rozwiązania problemów drogą rozumowania dedukcyjnego. Pojęcie programowania logicznego jest często źle zdefiniowane. Według Roberta Kowalskiego, będącego jednym z głównych twórców teorii programowania logicznego, opiera się ona na dwóch podstawowych założeniach:
* Traktowanie logiki jako języka programowania
* Oddzielenie logiki programu od sterowania
Prolog a programowanie w logice
Język programowania PROLOG będący jednym z najbardziej rozpowszechnionych systemów programowania w języku logiki oparty jest w zasadniczej części na języku klauzul Horna, który stanowi podzbiór języka klauzulowego postaci logiki.
Szereg technologii wykozystywanych jest w Prolog'u w celu ułatwienia programowania w logice. Należą do nich m.in. CLP,CLP(FD),CLP(QR),CHR.
Constraint logic programming -programowanie z ograniczeniami
Teoria
Programowanie logiczne z ograniczeniami (Constraint Logic Programming CLP) stało się w ostatnich latach popularnym sposobem modelowania i rozwiązywania wielu problemów z dziedziny:
sztucznej inteligencji
problemów kombinatorycznych
przetwarzania mowy
harmonogramowania
przetwarzania języków naturalnych (konstruowanie efektywnych parserów)
systemów baz danych (zapewnienie spójności danych)
biologii molekularnej (sekwencjonowanie DNA)
inżynierii elektronicznej (lokalizacja błędów)
projektowania obwodów drukowanych
Jego główną zaletą jest deklaratywność, czyli sformułowanie zadania jest od razu programem rozwiązującym to zadanie. Programowanie to bazuje na modelowaniu zadania jako problemu spełnienia ograniczeń (Constraint Satisfacton Problem CSP). Ograniczenia są zależne od dziedzin zmiennych, których dotyczą. Najpopularniejszą i pierwszą dziedziną zmiennych była skończona dziedzina liczb naturalnych. Innymi dziedzinami są: skończone zbiory, drzewa, rekordy, przedziały rzeczywiste. Najistotniejszą cechą i największą zaleta programowania z ograniczeniami jest ich propagacja .
Propagacja ograniczeń
Propoagacja ograniczeń sprawiła, że ta technika stała się najlepsza metodą dla wielu problemów kombinatorycznych. Zasadą działania propagacji jest usuwanie wartości nie spełniających ograniczeń z domen zmiennych. Języki do programowania z ograniczeniami mają możliwość wyrażania zmiennych z zakresu domen liczb naturalnych (najczęściej stosowane), przedziałów liczb rzeczywistych, zbiorów i innych.
Przykład:
x €{1..5}, y €{1..6}
Gdy na powyższe dwie zmienne wprowadzimy ograniczenie
x>y+1
, wtedy
propagacja ograniczeń zredukuje powyższe domeny do następujących wartości:
x €{3, 4, 5}, y €{1, 2, 3}
ponieważ wartości {1, 2} z domeny x nie spełniają ograniczenia x>y+1 dla żadnej z wartości z domeny y. Podobnie można rozpatrywać wartości {4, 5, 6} z domeny y. Jednak możemy wprowadzić takie ograniczenie jak x+y=6, które nie usuwa żadnych wartości z domen. Ograniczenia nie są zazwyczaj tak proste ja to przedstawiono, często łączą ze sobą wiele zmiennych, a metody usuwania poszczególnych wartości, zwane algorytmami filtracyjnymi są bardzo złożone. Sama propagacja z ograniczeniami rzadko daje rozwiązanie. Dlatego jest ona zawsze łączona z dystrybucją i poszukiwaniem.
Dystrybucja i poszukiwanie
W większości przypadków propagacja ograniczeń nie prowadzi do rozwiązania (jak to zostało przedstawione w powyższym przykładzie). Dlatego programowanie z ograniczeniami jest ściśle związane z dystrybucją połączoną z poszukiwaniem.
Dystrybucja polega na wprowadzeniu dodatkowego ograniczenia (często jest to przyporządkowanie jednej wartości do zmiennej, a zadaniem dystrybucji jest odpowiednie wybranie zmiennej i wartości). Kiedy to nastąpi sprawdzana jest spójność poprzez propagację ograniczeń i istnieją trzy możliwości:
Ten proces jest dokonywany iteracyjnie i jest nazywany poszukiwaniem. Poszukiwanie jest odpowiedzialne za zatrzymanie; po znalezieniu pierwszego rozwiązania lub pewnej liczby rozwiązań lub wszystkich rozwiązań. Poszukiwanie tworzy tzw. drzewo poszukiwań, gdzie każdy węzeł jest stanem zmiennej.
Ograniczenia
Wyróżniamy następujące ograniczenia:
arytmetyczne(porównywanie dwóch liczb: ≤, ≥, ≠,=,<,>)
logiczne:(#\ Q-zaprzeczenie, P #/\ Q -and, P#/Q -xor, P #\/ Q-or)
dziedziny ograniczone- np. liczby całkowite, naturalne, specyfikacja dziedziny poprzez wypisanie wszystkich elementów
drzewa i listy
Moduły CLP
Biblioteka CLP pojawiła się w SWI PROLOG od wersji 5.5.4, a od wersji 5.6.7 wprowadzono dodatkowe moduły, które rozszerzają jej funkcjonalność.
Poniżej przedstawię 4 podstawowe moduły:
clpfd (Constraint Programming Language over Finite Domains)
CLPFD jest modułem CLP i bazuje przede wszystkim na dziedzinie liczb całkowitych. Predykaty modułu umożliwiają m.in. określanie relacji/ograniczeń, konwersję wyrażeń do ich wartości liczbowej, tak że rozrastanie się wyrażeń może postępować we wszystkich kierunkach, systematyczne poszukiwanie rozwiązań. Wyrażeniem w module CLP(FD) może być liczba całkowita, zmienna.
Operacje które można wykonywać: dodawanie i odejmowanie wyrażeń, mnożenie, szukanie minimum lub maksimum dwóch wyrażeń, reszta z dzielenia wyrażeń przez siebie, wartość bezwzględna, dzielenie liczb całkowitych. Natomiast ograniczenia wynikające z relacji to, jak już wcześniej opisałam i przedstawiłam w tabelce: ≠ ,=,> , ≥ , < ,≤ .
Przykład
Poniższy przykład przedstawia wykorzystanie ograniczeń i porównywanie wyrażeń przy pomocy modułu CLP(FD).
Zagadka SEND+MORE=MONEY:
:- use_module(library(clpfd)).
puz([S,E,N,D,M,O,R,Y]) :-
Vars = [S,E,N,D,M,O,R,Y],
Vars ins 0..9,
all_different(Vars),
sum(S,E,N,D,M,O,R,Y).
sum(S,E,N,D,M,O,R,Y):-
S*1000 + E*100 + N*10 + D +M*1000 + O*100 + R*10 + E #= M*10000 + O*1000 + N*100 + E*10 + Y,
M #\= 0, S #\= 0.
Na początku inicjalizujemy moduł clpfd, a następnie tworzymy zmienne Vars I określamy, że powinny należeć do zbioru od 0..9. Var ins oznacza, że liczby będą dokładnie z zakresu od 0..9(jednocyfrowe) bez możliwości tworzenia liczb dwucyfrowych. All different(Vars ) zapewnia, że wszystkie zmienne będą różne.
clp_distinct
CLP_distinct jest to biblioteka, która dostarcza nam ograniczenia na zmienne. Określa w jakim przedziale powinny znajdować się zmienne np.
vars_in([X,Y,Z],[1,2,3])
Można także wywołać predykat, który określi, że zmienne powinny być różne:
All_distinct(Vars)
Aby otrzymać konkretne wartości, a nie przedziały, wtedy stosujemy predykat label/1.
Przykład:
[X,Y] in 1..3, vars_in([X, Y],[1, 2]), all_distinct([X, Y]), label([X, Y]).
Kolejny ciekawy predykat to All_different.
Przykład:
?- [X,Y,Z] in 0..1, all_different([X,Y,Z]).
X = _G180{0..1}
Y = _G183{0..1}
Z = _G186{0..1} ;
Jednak w przeciwieństwie do All_distinct, all_different nie wykrywa braku rozwiązania (patrz przykład powyżej). Dopiero po dodaniu predykatu label/1 wynik jest poprawny-false.
CLP(Q,R) Constraint Logic Programming over Rationals or Reals
CLP(Q,R) Constraint Logic Programming over Rationals or Reals jest to kolejny moduł, który ułatwia programowanie z ograniczeniami. Służy on do modelowania problemów na zbiorze liczb rzeczywistych i wymiernych. Biblioteka CLP(Q,R) składa się z dwóch modułów:
use_module(library(clpq))
use_module(library(clpr))
Większość predykatów dla modułu CLP(Q) oraz CLP(R) są takie same i należą do nich:
| Predykaty | Opis |
| + Expr | unary plus |
| - Expr | unary minus |
| Expr + Expr | addition |
| Expr - Expr | subtraction |
| Expr * Expr | multiplication |
| Expr / Expr | division |
| abs(Expr) | absolute value |
| sin(Expr) | trigonometric sine |
| cos(Expr) | trigonometric cosine |
| tan(Expr) | trigonometric tangent |
| pow(Expr,Expr) | raise to the power |
| exp(Expr,Expr) | raise to the power |
| min(Expr,Expr) | minimum of the two arguments |
| max(Expr,Expr) | maximum of the two arguments |
Ograniczenia:
| Ograniczenia | Opis |
| Expr =:= Expr | equation |
| Expr = Expr | equation |
| Expr < Expr | strict inequation |
| Expr > Expr | strict inequation |
| Expr =< Expr | nonstrict inequation |
| Expr >= Expr | nonstrict inequation |
| Expr =\= Expr | disequation |
Wyjątek pomiędzy bibliotekami stanowi predykat: bb_inf/4 w CLP(Q) i bb_inf/5 w CLP(R).Predykaty te obliczają kres dolny wyrażenia. Różnią się jedynie tym, że dla liczb rzeczywistych określamy jeszcze zakres dla którego liczba będzie zaokrąglana do liczby całkowitej.
Używanie dwóch bibliotek jest dozwolone w jednym programie, jednak trzeba je zadeklarować oddzielnie. Błędy w działaniu programu pojawiają się, gdy dla tych samych zmiennych stosujemy predykaty z różnych bibliotek.
Wady CLP
Biblioteka CLP pomimo swojej złożoności i wielu dodatkowych modułów z których programiści mogą korzystać często nie wystarcza by szybko i wydajnie rozwiązywać złożone problemy.
W celu zmodyfikowania istniejących ograniczeń lub stworzenia nowych, dokładniejszych reguł został stworzony specjalny język programowania CHR (z ang. Constraint Handling Rules), który umożliwia szybsze tworzenie programów i ich optymalizację.
CHR -Constraint Handling Rules
CHR jest deklaratywnym językiem programowania, który został stworzony przez Thom Frühwirth w 1991 roku. Jest używany jako język wysokiego poziomu do rozwiązywania takich problemów jak:
Język Constraint Handling Rules jest zaimplementowany w SWI-Prologu i dostępny od wersji 5.6.0.
Dołączenie biblioteki następuje poprzez:
:- use_module(library(chr)).
Przykład:
Ponizszy przykład przedstawia zasadę działania CHR. Pokazuje w jaki sposób określić znak nierówności ≤ (http://www.sics.se/sicstus/docs/3.7.1/html/sicstus_34.html#SEC290):
:- use_module(library(chr)).
handler leq.
constraints leq/2.
:- op(500, xfx, leq).
reflexivity @ X leq Y <=> X=Y | true.
antisymmetry @ X leq Y , Y leq X <=> X=Y.
idempotence @ X leq Y \ X leq Y <=> true.
transitivity @ X leq Y , Y leq Z ==> X leq Z.
Jak widzimy reguła składa się z 4 części : zwrotności, antysymetrii, idempotentności i przechodniości. Ich nazwy poprzedzają znak @, a po nich występują predykaty zdefiniowane przez użytkownika (heads), wbudowane (guards) lub oba rodzaje ograniczeń (body), definiujące własności relacji.
Ciekawy jest sposób wywołania funkcji:
?- leq(X,Y), leq(Y,Z).
Jako wynik działania otrzymujemy Yes, co oznacza, że dla X≤Y, Y≤Z to X≤Z.
Program z przykładami
Implementacja
Projekt został napisany w Javie z wykorzystaniem SWI Prolog’u.
Funkcje, które realizuje aplikacja to:
* Obliczanie wartości silni
Obliczanie n-tego wyrazu ciągu Fibonacciego
Obliczanie pierwiastków równania kwadratowego
Obliczanie kolorów dla 6 zdefiniowanych państw
Problem plecakowy
Problem n-królowej
Interfejs użytkownika
Interfejs użytkownika został stworzony przy pomocy biblioteki SWING.
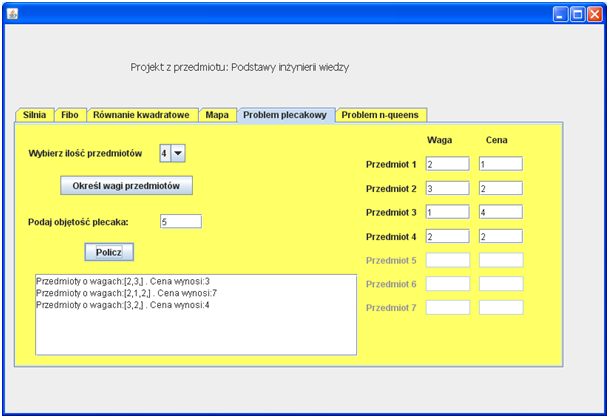
 Wynik działania dla problemu plecakowego:
Wynik działania dla problemu plecakowego:
Sekwencjonowanie DNA
Teoria
Implementacja sekwencjonowania DNA w PROLOGu
Wybór środowiska
Interfejs użytkownika
Podsumowanie

